《解直角三角形（3）》教学课件.pptVIP免费

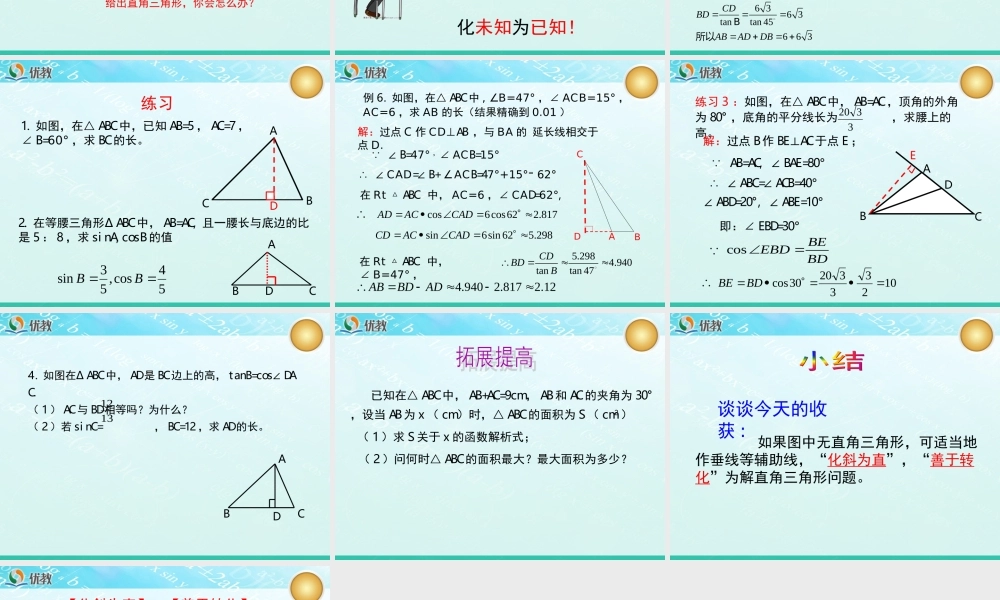
2.4解直角三角形第3课时1.直角三角形中元素之间的关系（1）.两锐角之间的关系:∠A+∠B=90°（2）.三边之间的关系:a2+b2=c2（3）.边角之间的关系：cabCABcaAA斜边的对边sincb斜边邻边AAcosbaAAA的邻边的对边tan2.在直角三角形中，由已知的，求出另一些的过程，叫做解直角三角形.3.如果知道直角三角形的几个元素就可以求其他的元素？有几种情况？两个元素（至少一个是边）两条边或一边一角一些边、角边、角求下列各直角三角形中字母的值．上节课我们已经学过：1.已知两边解直角三角形.2.已知一条边和一个锐角解直角三角形.想一想：如果已知条件中，没有直接给出直角三角形，你会怎么办？例5.如图,在△ABC中,已知∠A60°,∠B﹦﹦45°,AC12,﹦求AB的长.ACBD∆ABC不是直角三角形怎么办？转化思想：作AB边上的高，把锐角三角形转化为直角三角形，把问题转化为解直角三角形！化未知为已知！ACBD12,60.3sin12sin6012632在t中，RACDACACDACA1cos12601262cosADACA45636363tantan45663tBRBCDBCDCDBDABADDB在中，由，，得所以解：过点C作CD⊥AB，垂足为点D.例5.如图,在△ABC中,已知∠A60°,∠B﹦﹦45°,AC12,﹦求AB的长.54cos,53sinBB1.如图，在△ABC中，已知AB=5，AC=7，∠B=60°，求BC的长。ABCD练习2.在等腰三角形∆ABC中，AB=AC,且一腰长与底边的比是5：8，求sinA,cosB的值ABCD例6.如图，在△ABC中,∠B=47°，∠ACB=15°，AC=6，求AB的长（结果精确到0.01）解：过点C作CD⊥AB，与BA的延长线相交于点D.∵∠B=47°，∠ACB=15°∴∠CAD=∠B+∠ACB=47°+15°=62°在Rt△ABC中，AC=6，∠CAD=62°,∴CDAB在Rt△ABC中，∠B=47°，4.9402.8172.12ABBDAD5.2984.940tantan47CDBDB817.262cos6cosCADACAD298.562sin6sinCADACCD练习3：如图，在△ABC中，AB=AC，顶角的外角为80°，底角的平分线长为，求腰上的高。3320EDCBA解：过点B作BE⊥AC于点E；∵AB=AC,∠BAE=80°∴∠ABC=∠ACB=40°∠ABD=20°,∠ABE=10°即：∠EBD=30°BDBEEBDcos∵1023332030cosBDBE∴4.如图在∆ABC中，AD是BC边上的高，tanB=cos∠DAC.（1）AC与BD相等吗？为什么？（2）若sinC=，BC=12，求AD的长。1312CABD已知在△ABC中，AB+AC=9cm，AB和AC的夹角为30°，设当AB为x（cm）时，△ABC的面积为S（cm2）（1）求S关于x的函数解析式；（2）问何时△ABC的面积最大？最大面积为多少？如果图中无直角三角形，可适当地作垂线等辅助线，“化斜为直”，“善于转化”为解直角三角形问题。谈谈今天的收获:【化斜为直】，【善于转化】DCFEABDCFEABDCFEABDCFEAB四个解直角三角形的典型变式图形