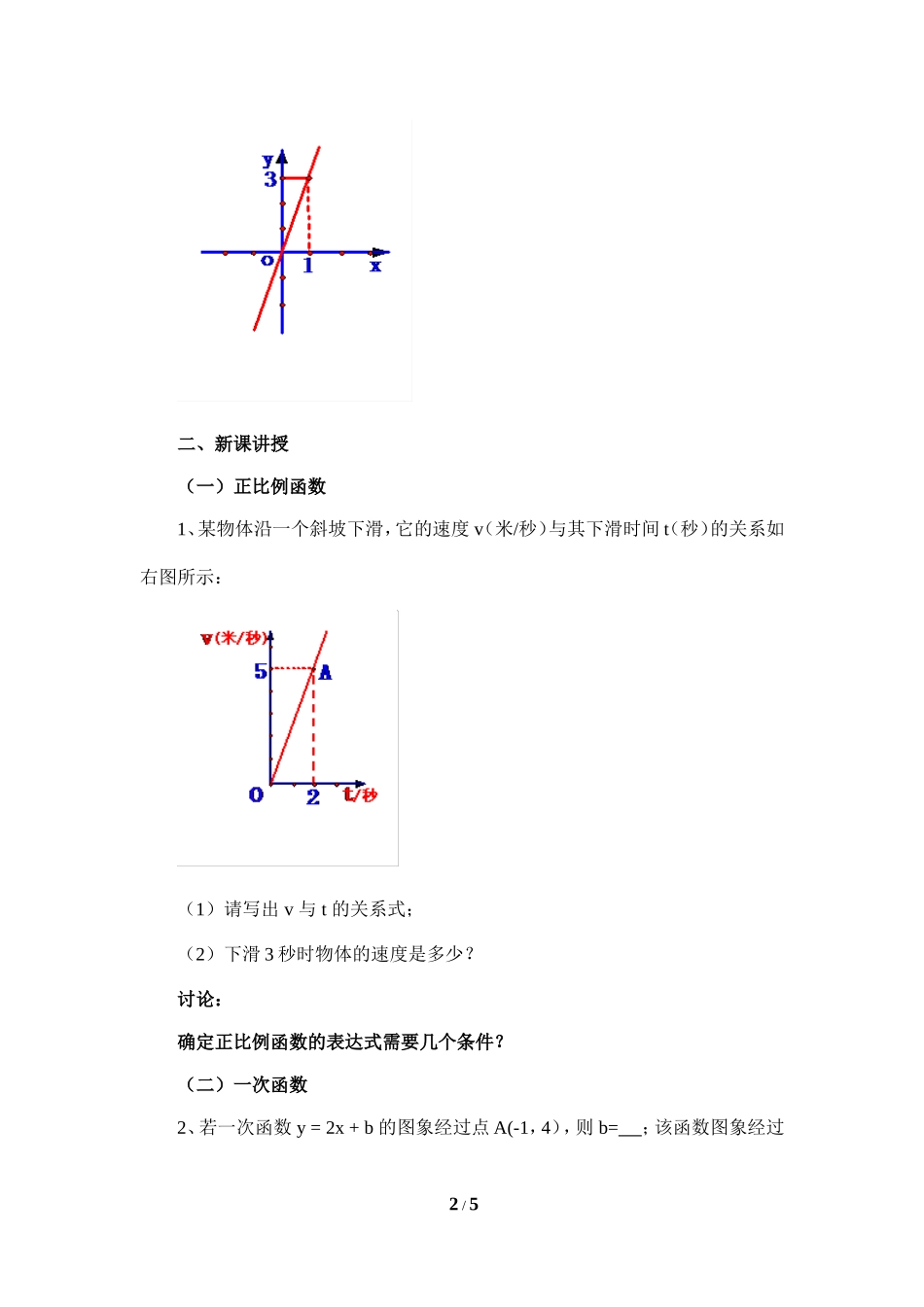
6.4确定一次函数的表达式教学目标:(一)知识与能力1.了解一个条件确定一个正比例函数,两个条件确定一个一次函数。2.会用待定系数法求出一次函数和正比例函数表达式。(二)过程与方法:1.复习一次函数做图象的方法,引出由图象来确定关系式,进而确定一次函数表达式的问题,体现了数形结合的思想。2.通过例题讲解,根据函数的图象与函数关系式的关系,明确求一次函数表达式的方法。(三)情感态度与价值观1.通过探究,引出一次函数表达式,培养学生的逆向思维。2.学会求一次函数及其他函数表达式的一般方法。教学重难点:重点:会用待定系数法确定一次函数表达式;难点:能够根据一次函数图象或者其他一些情境,熟练灵活地利用待定系数法确定函数的表达式。教学方法:引导探究、合作交流。学法指导:让学生在回顾已学内容的基础上通过“数”与“形”的相互转化来确定一次函数的表达式。在练习的过程中相互交流来加以巩固。教学过程:一、回顾导入若小明画了如图所示的一条直线,你能知道他画的直线的表达式是什么吗?1/5二、新课讲授(一)正比例函数1、某物体沿一个斜坡下滑,它的速度v(米/秒)与其下滑时间t(秒)的关系如右图所示:(1)请写出v与t的关系式;(2)下滑3秒时物体的速度是多少?讨论:确定正比例函数的表达式需要几个条件?(二)一次函数2、若一次函数y=2x+b的图象经过点A(-1,4),则b=;该函数图象经过2/5点B(1,_)和点C(_,0)。3、假如又有同学画了如下一条直线,你能知道该函数的表达式吗?想一想:确定一次函数的表达式需要几个条件?(三)例题例1在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数。一根弹簧不挂物体时长14.5cm;当所挂物体的质量为3kg时,弹簧长16cm。请写出y与x之间的关系式,并求当所挂物体的质量为4kg时弹簧的长度。解:设y=kx+b,根据题意,得14.5=b①16=3k+b②将b=14.5代入②,得k=0.5。在弹性限度内,y于x的关系是为:y=0.5x+14.5当x=4时,y=0.5×4+14.5=16.5(cm)即物体的质量为4kg时,弹簧长度为16.5cm。(四)巩固练习3/5练习(A)1、根据条件确定一次函数的表达式:y是x的正比例函数,当x=2时,y=6,求y与x之间的关系式。2、直线l是一次函数y=kx+b的图象,(1)k=,b=。(2)当x=30时,y=。(3)当y=30时,x=。练习(B)1、已知,一次函数的图象与直线y=2x平行,且过点(-1,1),试求这个一次函数的表达式。2、若函数y=kx+b的图象经过点(0,-1),(-3,2),求k,b的...