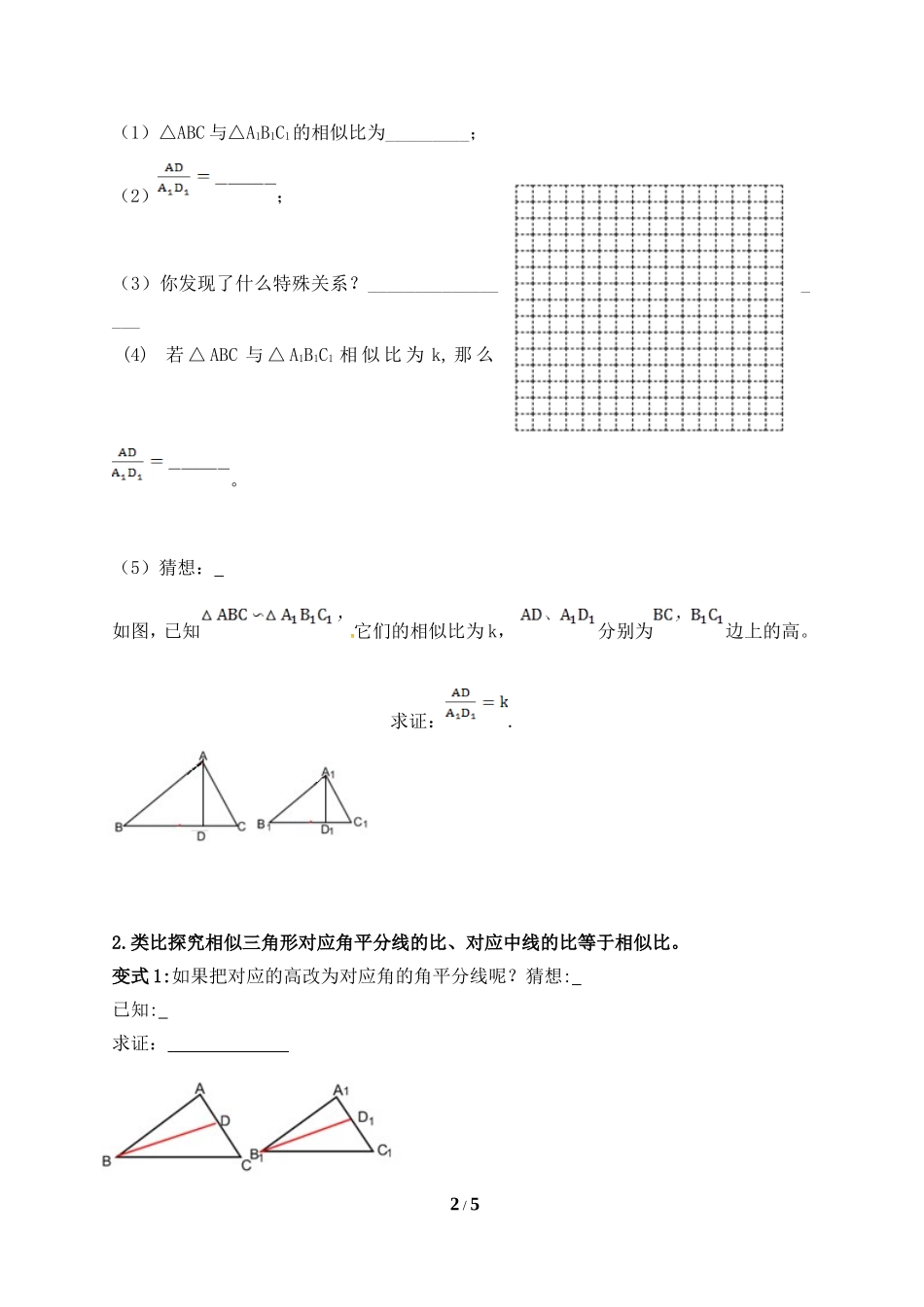
相似三角形的性质(1)导学案态度就是竞争力,积极的学习态度就是你脱颖而出的砝码【学习目标】:1.掌握相似三角形的性质的对应高,对应中线,对应角平分线的比存在的等量关系。2.进一步巩固三角形相似的判定定理,并能进行相应性质的推导。3.能熟练运用三角形相似的性质进行量的计算。4.经历讨论与交流,猜想与验证,发展说理习惯,在观察、操作、推理、归纳等探索过程中,提高学习数学的兴趣和自信心。【学习重点】:相似三角形的性质【难点】:探究相似三角形的性质【学习方法】:小组合作学习探究【学习过程】:模块一预习反馈一、旧知链接1.相似三角形的定义三角对应,三边对应的两个三角形。叫做相似比。2.相似三角形的判定方法①的两个三角形相似;②的两个三角形相似;③的两个三角形相似。3.当两个相似三角形相似比为1时,两个三角形4.全等三角形性质:全等三角形的对应边对应角;对应高、对应中线、对应角平分线分别_______。5.根据相似三角形的定义,得到相似三角形的性质三角________,三边___________两个三角形相似除了上述性质,我们还可以得到哪些结论呢?这就是我们这节课所要学习的相似三角形的性质。二、自学探究实验、猜想、证明:相似三角形对应高的比等于相似比1.在方格纸中画出一对相似三角形△ABC∽△A1B1C1,AD,A1D1,分别为BC,B1C1,边上的高。1/5(1)△ABC与△A1B1C1的相似比为_________;(2);(3)你发现了什么特殊关系?__________________(4)若△ABC与△A1B1C1相似比为k,那么。(5)猜想:如图,已知它们的相似比为k,分别为边上的高。求证:.2.类比探究相似三角形对应角平分线的比、对应中线的比等于相似比。变式1:如果把对应的高改为对应角的角平分线呢?猜想:已知:求证:2/5结论:____________________________________________________________变式2:如果把对应的高改为对应边上的中线呢?猜想:已知:求证:结论:____________________________________________________________________相似三角形的性质:相似三角形的、、等于相似比。几何语言: △ABC∽△A1B1C1,,AD,A1D1,分别为对应高,AE,A1E1,分别为对应角平分线,AF,A1F1,分别为对应中线,∴===模块二合作探究探究1.如图在△ABC中,AD是△ABC的高,点P、Q在BC上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.(1)△ASR与△ABC相似吗?为什么?(2)求正方形PQRS的边长?3/5探究2.如图,已知,的相似比为k。(1)若,,则等于多少?...