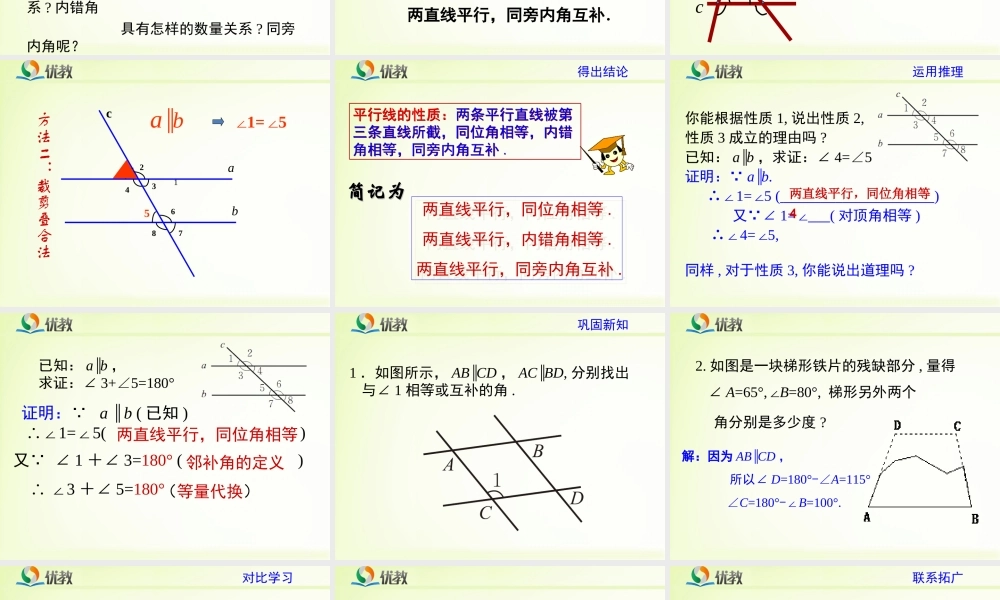
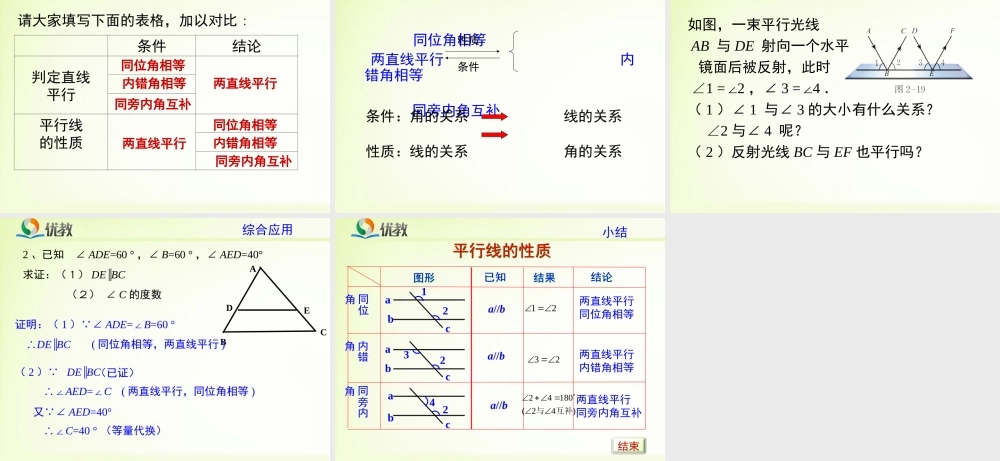
acb1.经历探索直线平行的性质的过程,掌握平行线的三条性质.2.能运用三条性质进行简单的推理和计算.学习目标(1)因为∠1=5(∠已知)所以a∥b()(2)因为∠4=∠(已知)所以a∥b(内错角相等,两直线平行)(3)因为∠4+∠=180°(已知)所以a∥b()同位角相等,两直线平行56同旁内角互补,两直线平行温故知新如图,直线a与直线b平行(1)测量同位角∠1和∠5的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?(2)图中有几对内错角?它们的大小有什么关系?为什么?(3)图中有几对同旁内角?它们的大小有什么关系?为什么?探求新知角∠1∠2∠3∠4∠5∠6∠7∠8度数活动1:同学们可以先测量这些角的度数,把结果填入下表内.活动2:请同学们根据测量所得的结果猜想:同位角具有怎样的数量关系?内错角具有怎样的数量关系?同旁内角呢?动动小手猜想结论两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.活动3:另外画一组平行线被第三条直线所截,同样测量并计算各角的度数,检验刚才的猜想是否成立?如果直线a与b不平行,猜想还成立吗?试一试.ba1c除了测量的方法来说明平行线的方法,还有其他的方法吗?验证猜想1b567ac24381∠1=5∠a∥b方法二:裁剪叠合法平行线的性质:两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.平行线的性质:两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.简记为简记为两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.得出结论你能根据性质1,说出性质2,性质3成立的理由吗?已知:a∥b,求证:∠4=5∠证明: a∥b.∴∠1=5(∠)又 ∠1=∠(对顶角相等)∴∠4=5,∠同样,对于性质3,你能说出道理吗?两直线平行,同位角相等4运用推理已知:a∥b,求证:∠3+5=180°∠证明: a∥b(已知)∴∠1=∠5()又 ∠1+∠3=180°()∴∠3+∠5=180°两直线平行,同位角相等邻补角的定义(等量代换)巩固新知1.如图所示,AB∥CD,AC∥BD,分别找出与∠1相等或互补的角.2.如图是一块梯形铁片的残缺部分,量得∠A=65°,∠B=80°,梯形另外两个角分别是多少度?解:因为ABCD∥,所以∠D=180°-∠A=115°∠C=180°-∠B=100°.对比学习请大家填写下面的表格,加以对比:条件结论判定直线平行平行线的性质同位角相等两直线平行内错角相等同旁内角互补两直线平行...