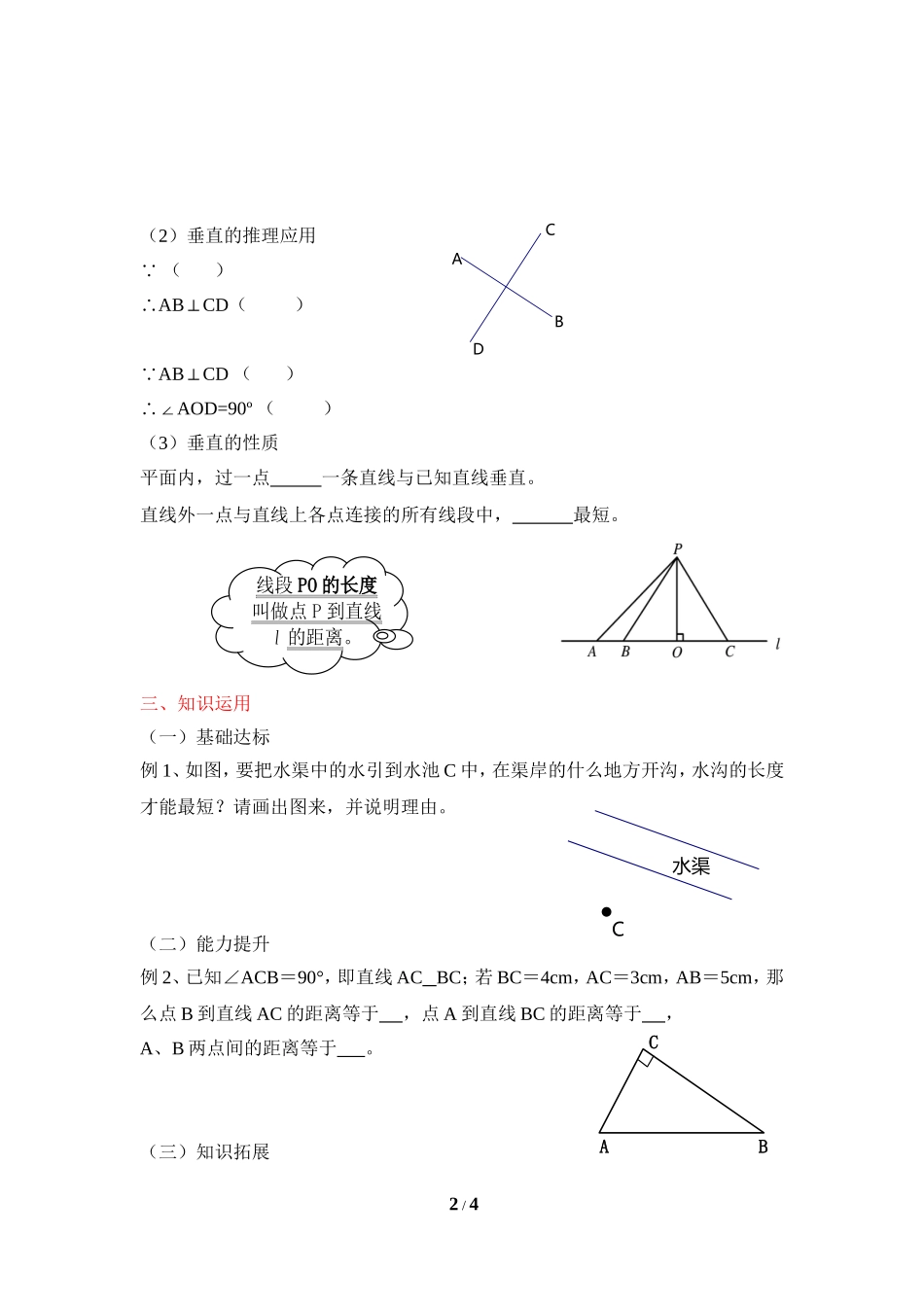
导学案【课题】7.1两条直线的位置关系(2)【学习目标】1、了解垂直的概念,能说出垂线的性质;2、会用三角尺或量角器过一点画一条直线的垂线。【学习重点】垂直的概念,垂线的性质【学习过程】一、知识预备互余互补对顶角对应图形数量关系性质二、知识研究预习书67-68页1、如图,已知∠1=60º,那么∠2=,∠3=,∠4=。改变图中∠1的大小,若∠1=90º,那么∠2=,∠3=,∠4=。这时两条直线的关系是,这是两条直线相交的特殊情况。2、垂直(1)定义及表示方法两条直线相交,所成的四个角中有一个角是时,称这两条直线互相,其中一条直线叫做另一条直线的垂线,它们的交点叫做。垂直用符号“⊥”来表示。1/4ba432113∠与∠42421ODCBA记作l⊥m,垂足为点O.记作AB⊥CD,垂足为点O.(2)垂直的推理应用∵()∴AB⊥CD()∵AB⊥CD()∴∠AOD=90º()(3)垂直的性质平面内,过一点一条直线与已知直线垂直。直线外一点与直线上各点连接的所有线段中,最短。三、知识运用(一)基础达标例1、如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。(二)能力提升例2、已知∠ACB=90°,即直线ACBC;若BC=4cm,AC=3cm,AB=5cm,那么点B到直线AC的距离等于,点A到直线BC的距离等于,A、B两点间的距离等于。(三)知识拓展2/4线段PO的长度叫做点P到直线l的距离。DCBAABC水渠C例3、点C在直线AB上,过点C引两条射线CE、CD,且∠ACE=32°,∠DCB=58°,则CE、CD有何位置关系关系?为什么?四、巩固练习:A组1、∠BAC=90°,AD⊥BC于点D,则下面结论中正确的有()个。①点B到AC的垂线段是线段AB;②线段AC是点C到AB的垂线段;③线段AD是点A到BC的垂线段;④线段BD是点B到AD的垂线段。A、1个;B、2个;C、3个;D、4个。B组2、如图中,点O在直线AB上,OEAB⊥于点O,OCOD,⊥若∠DOE=320,请你求出∠EOC、∠BOD的度数,并说明理由。3、如图中,点O在直线AB上,OC平分∠BOD,OE平分∠AOD,则OE和OC有何位置关系?请简述你的理由。五、课堂反思:1、今天,你学习了什么知识?2、对今天的课,你还有哪些困惑?【课后练习】A组3/4DCBAEOABCDE3题O2题DECBA1、已知钝角∠AOB,点D在射线OB上(1)画直线DEOB⊥(2)画直线DFOA⊥,垂足为FB组2、如图,OAOC⊥,OBOD⊥,∠BOC=30°,求∠AOB,∠COD,∠AOD。C组3、如图,AOOB⊥,OD平分∠AOC,∠BOC=150°,求∠DOC的度数。4/4ODBAODCBAODCBA