第1课时 相似三角形的判定（1）.pptxVIP免费

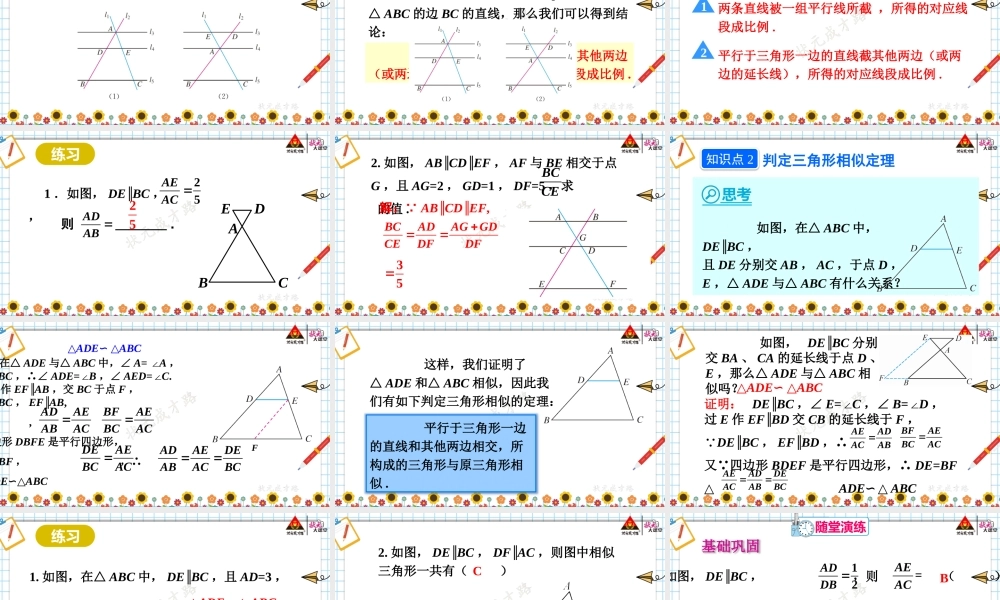
状元成才路状元成才路27.2.1相似三角形的判定第1课时相似三角形的判定（1）R·九年级下册27.2相似三角形新课导入问题1：我们学过哪些判定两个三角形全等的方法？SSS，SAS，ASA，AAS问题2：类比上面这些方法，猜一猜判定两个三角形相似的方法有哪些？推进新课相似三角形知识点1在相似多边形中，最简单的就是相似三角形.∠A=∠A'，∠B=∠B'，∠C=∠C'．ABACBCkABACBC''''''在△ABC和△A'B'C'中，如果我们就说△ABC和△A'B'C'相似，相似比为k，相似符号为“∽”.如果k=1，这两个三角形有怎样的关系？全等两个直角三角形一定相似吗？两个等腰直角三角形呢？30°45°两个直角三角形不一定相似两个等腰直角三角形一定相似思考两个等腰三角形一定相似吗？两个等边三角形呢？两个等腰三角形不一定相似两个等边三角形一定相似判定两个三角形全等时，除了可以验证它们所有的角和边分别相等外，还可以使用简便的判定方法（SSS，SAS，ASA，AAS）．类似地，判定两个三角形相似时，是不是也存在简便的判定方法呢？我们先来探究下面的问题.自由讨论探究如图，任意两条直线l1，l2，再画三条与l1，l2都相交的平行线l3，l4，l5．分别度量l3，l4，l5在直线l1上截得的两条线段AB，BC和在l2上截的得两条线段DE，EF的长度，与相等吗？任意平移l5，与还相等吗？ABBCDEEFABBCDEEF可以发现，当l3∥l4∥l5时，有ABDEBCEFBCEFABDEABDEACDFBCEFACDF一般地，我们有平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例.状元成才路把平行线分线段成比例的基本事实应用到三角形中，会出现下面两种情况:在图1中，把l4看成平行于△ABC的边BC的直线；在图2中，把l3看成平行于△ABC的边BC的直线，那么我们可以得到结论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例.两条直线被一组平行线所截，所得的对应线段成比例.平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例.12练习1．如图，DE∥BC，，则________．AEAC25ADABABCED252.如图，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，求的值.BCCE解： AB∥CD∥EF,BCADAGGDCEDFDF35判定三角形相似定理知识点2思考如图，在△ABC中，DE∥BC，且DE分别交AB，AC，于点D，E，△ADE与△ABC有什么关系？△ADE∽△ABC在△ADE与△ABC中，∠A=∠A，BC，∴∠ADE=∠B，∠AED=∠C.作EF∥AB，交BC于点F，BC，EF∥AB,,边形DBFE是平行...