24.4 弧长和扇形面积 (第1课时）.pptxVIP免费

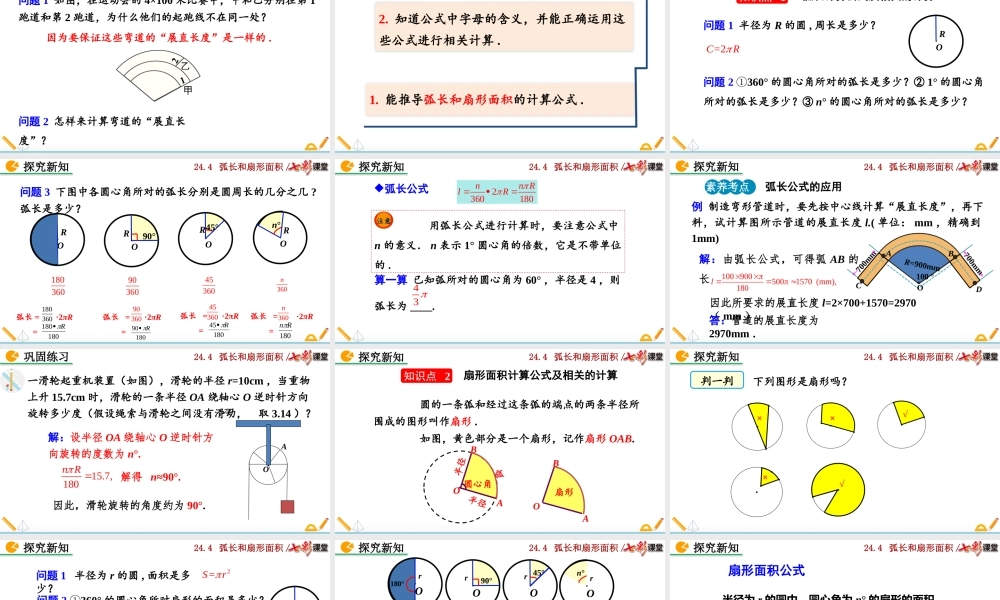
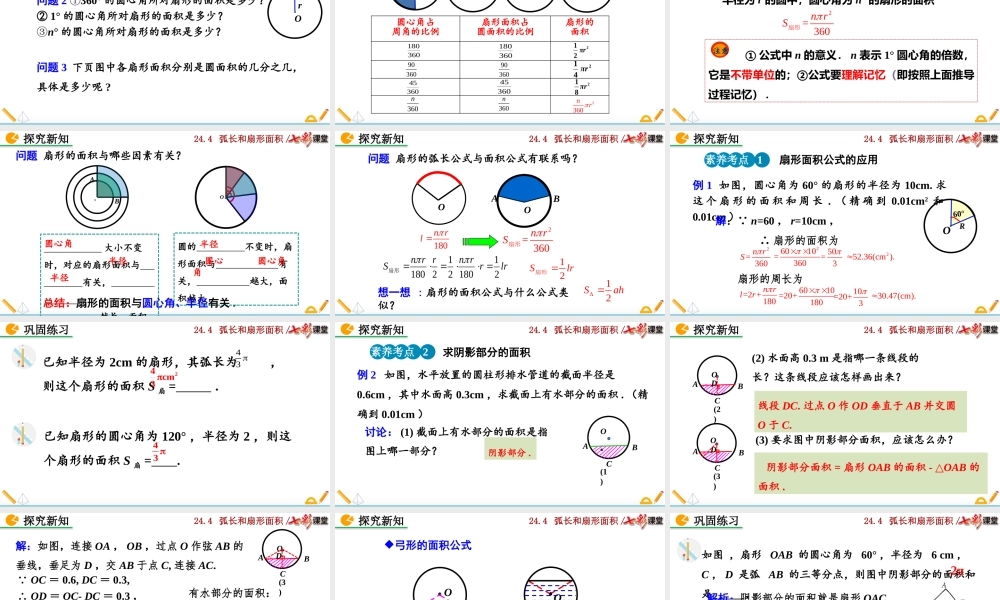
24.4弧长和扇形面积/24.4弧长和扇形的面积（第1课时）人教版数学九年级上册24.4弧长和扇形面积/问题1如图，在运动会的4×100米比赛中，甲和乙分别在第1跑道和第2跑道，为什么他们的起跑线不在同一处？问题2怎样来计算弯道的“展直长度”？因为要保证这些弯道的“展直长度”是一样的.导入新知24.4弧长和扇形面积/2.知道公式中字母的含义，并能正确运用这些公式进行相关计算.1.能推导弧长和扇形面积的计算公式.素养目标24.4弧长和扇形面积/问题1半径为R的圆,周长是多少？OR=2CR问题2360°①的圆心角所对的弧长是多少？②1°的圆心角所对的弧长是多少？③n°的圆心角所对的弧长是多少？探究新知弧长计算公式及相关的计算知识点124.4弧长和扇形面积/弧长=·2πR=弧长=·2πR=弧长=·2πR=弧长=·2πR=问题3下图中各圆心角所对的弧长分别是圆周长的几分之几?弧长是多少？OR180°OR90°OR45°ORn°探究新知180360180360180180R903609036018090R453604536018045R360n360n180Rn24.4弧长和扇形面积/用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的.注意算一算已知弧所对的圆心角为60°，半径是4，则弧长为____.432360180nnRlR弧长公式探究新知24.4弧长和扇形面积/例制造弯形管道时，要先按中心线计算“展直长度”，再下料，试计算图所示管道的展直长度l.(单位：mm，精确到1mm)解：由弧长公式，可得弧AB的长1009005001570(mm),180l因此所要求的展直长度l=2×700+1570=2970（mm）.答：管道的展直长度为2970mm．700mm700mmR=900mm(100°ACBDO700mm弧长公式的应用素养考点探究新知24.4弧长和扇形面积/解：设半径OA绕轴心O逆时针方向旋转的度数为n°.解得n≈90°.因此，滑轮旋转的角度约为90°.15.7,180nR一滑轮起重机装置（如图），滑轮的半径r=10cm，当重物上升15.7cm时，滑轮的一条半径OA绕轴心O逆时针方向旋转多少度（假设绳索与滑轮之间没有滑动，取3.14）？巩固练习·OA24.4弧长和扇形面积/圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.如图，黄色部分是一个扇形，记作扇形OAB.半径半径OBA圆心角弧OBA扇形探究新知扇形面积计算公式及相关的计算知识点224.4弧长和扇形面积/下列图形是扇形吗？判一判√×××√探究新知24.4弧长和扇形面积/问题1半径为r的圆,面积是多少？Or2=Sr问题3下页图中各扇形面积分别是圆面积的几分之几，具体是多少呢?问题236...