二次函数的图象与性质 课件设计.pptVIP免费

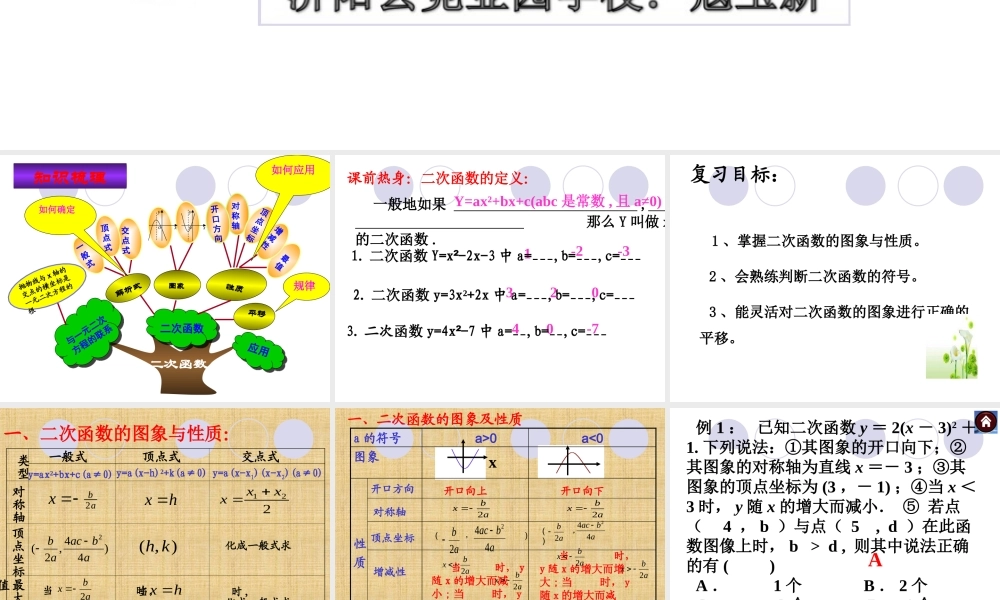
九年级复习------最值二次函数应用性质图象开口方向一般式顶点式交点式xyoxyo顶点坐标对称轴增减性二次函数与一元二次方程的联系解析式抛物线与x轴的交点的横坐标是一元二次方程的根知识梳理平移如何确定如何应用规律一般地如果,那么Y叫做x的二次函数.Y=ax²+bx+c(abc是常数,且a≠0)1-2-32.二次函数y=3x²+2x中a=___,b=___,c=___32040-71.二次函数Y=x²-2x-3中a=___,b=___,c=___课前热身：二次函数的定义：3.二次函数y=4x²-7中a=__,b=__,c=___复习目标：1、掌握二次函数的图象与性质。2、会熟练判断二次函数的符号。3、能灵活对二次函数的图象进行正确的平移。一、二次函数的图象与性质：y=ax²+bx+c(a≠0)类型y=a(x-h)²+k(a≠0)y=a(x-x1)(x-x2)(a≠0)一般式顶点式交点式对称轴顶点坐标最大(小)值abx2hx221xxx)44,2(2abacab),(khabacyabx4422当时,最值化成一般式求化成一般式求当时,最值y=khxx性质图象a<0a>0a的符号开口方向对称轴顶点坐标增减性最值一、二次函数的图象及性质开口向上开口向下abx2abx2ab2(，)abac442ab2(，)abac442当时,y有最小值为abac442abx2abac442当时,y最大值为abx2当时，y随x的增大而减小;当时，y随x的增大而增大.abx2abx2当时，y随x的增大而增大;当时，y随x的增大而减小.abx2abx2例1：已知二次函数y＝2(x－3)2＋1.下列说法：①其图象的开口向下；②其图象的对称轴为直线x＝－3；③其图象的顶点坐标为(3，－1)；④当x＜3时，y随x的增大而减小．⑤若点（4，b）与点（5,d）在此函数图像上时，b>d,则其中说法正确的有()A．1个B．2个C．3个D．4个A1.二次函数y=2(x-3)²+7的图象顶点坐标是——，对称轴是———2.二次函数y=3(x+1)²-5顶点坐标是———，对称轴是———3.抛物线y=x2+2x-4的开口方向是,对称轴是,顶点坐标是.4.已知二次函数y=x2-6x+m的最小值是1,那么m的值是.(3,7)X=3(-1,-5)X=-1针对训练:向上X=-1（－1，－5）10二、二次函数y=ax²+bx+c（a≠0）的图象特征与a、b、c、Δ的关系项目字母的符号图象的位置（特征）abcΔa>0a<0开口向上开口向下b=0对称轴是y轴对称轴在y轴左侧ab>0ab<0对称轴在y轴右侧c=0经过原点c>0c<0与y轴正半轴相交与y轴负半轴相交Δ=0Δ<0Δ>0与x轴有唯一交点（顶点）与x轴有两个交点与x轴没有交点※a+b+c的符号——>看x=1时，在图象上所对应的Y值；※a-b+c的符号——>看x=-1时，在图象上所对应的Y值；※2a+b的符号——>对...