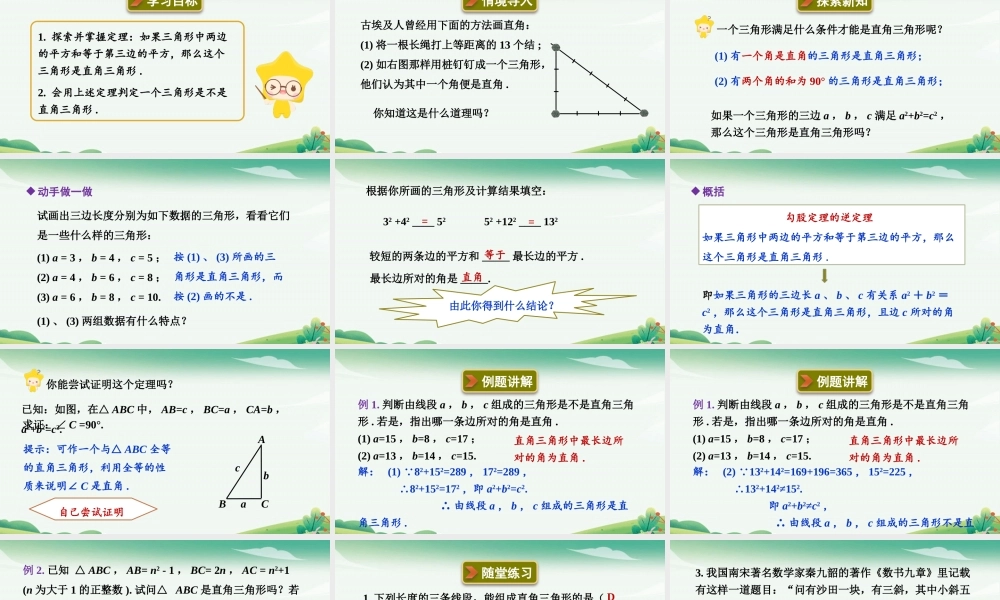
2.7探索勾股定理第2课时勾股定理的逆定理学习目标1.探索并掌握定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.2.会用上述定理判定一个三角形是不是直角三角形.古埃及人曾经用下面的方法画直角:(1)将一根长绳打上等距离的13个结;(2)如右图那样用桩钉钉成一个三角形,他们认为其中一个角便是直角.你知道这是什么道理吗?情境导入探索新知一个三角形满足什么条件才能是直角三角形呢?(1)有一个角是直角的三角形是直角三角形;(2)有两个角的和为90°的三角形是直角三角形;如果一个三角形的三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形吗?试画出三边长度分别为如下数据的三角形,看看它们是一些什么样的三角形:(1)a=3,b=4,c=5;(2)a=4,b=6,c=8;(3)a=6,b=8,c=10.动手做一做按(1)、(3)所画的三角形是直角三角形,而按(2)画的不是.(1)、(3)两组数据有什么特点?32+42____52较短的两条边的平方和_____最长边的平方.等于最长边所对的角是_____.直角52+122____132根据你所画的三角形及计算结果填空:==由此你得到什么结论?概括勾股定理的逆定理如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.即如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角.提示:可作一个与△ABC全等的直角三角形,利用全等的性质来说明∠C是直角.你能尝试证明这个定理吗?已知:如图,在△ABC中,AB=c,BC=a,CA=b,a2+b2=c2.求证:∠C=90°.abBCAc自己尝试证明例1.判断由线段a,b,c组成的三角形是不是直角三角形.若是,指出哪一条边所对的角是直角.(1)a=15,b=8,c=17;(2)a=13,b=14,c=15.解:(1)8 2+152=289,172=289,∴82+152=172,即a2+b2=c2.∴由线段a,b,c组成的三角形是直角三角形.直角三角形中最长边所对的角为直角.例题讲解例1.判断由线段a,b,c组成的三角形是不是直角三角形.若是,指出哪一条边所对的角是直角.(1)a=15,b=8,c=17;(2)a=13,b=14,c=15.直角三角形中最长边所对的角为直角.例题讲解解:(2)13 2+142=169+196=365,152=225,∴132+142≠152.即a2+b2≠c2,∴由线段a,b,c组成的三角形不是直例2.已知△ABC,AB=n2-1,BC=2n,AC=n2+1(n为大于1的正整数).试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由.∴△ABC是直角三角形,边AC所对的角是直角.解: AB2+BC2=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1=(...