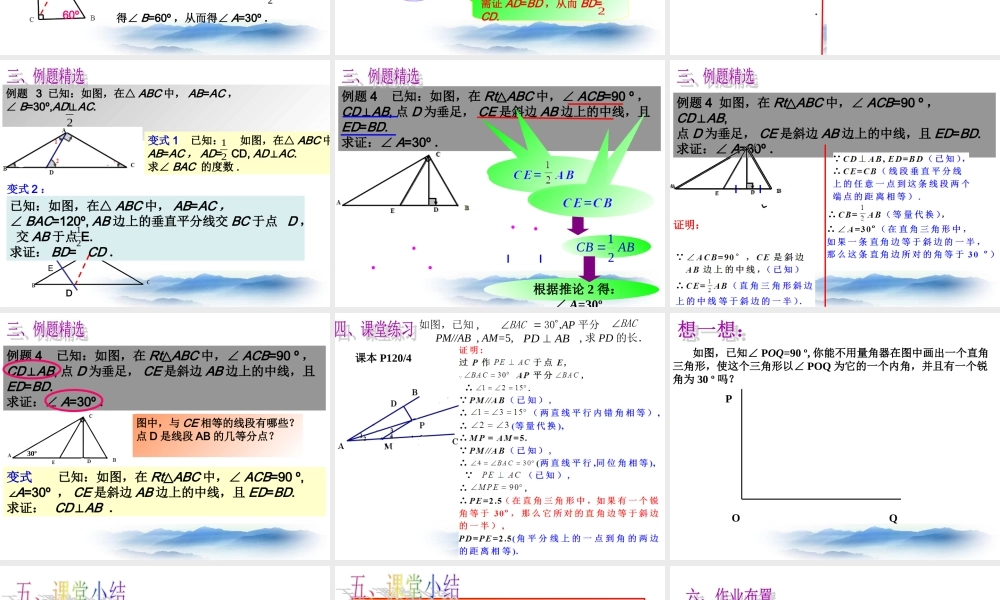
思考:已知Rt△ABC中,∠ACB=90°,CD为斜边AB上的中线,图中有几个等腰三角形?为什么?有两个等腰三角形,分别是△ACD和△DCB.“直角三角形斜边上的中线等于斜边的一半”,即CD=AD=BD=AB.21若再添加条件∠A=30º,则△DCB是什么特殊的三角形?边BC与AB之间有怎样的数量关系?你能归纳出这一结论吗?在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.BC=AB.21求证:在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.已知:Rt△ABC中,∠ACB=90º,∠A=30º.求证:BC=AB.21D已知:RtABC△中,∠ACB=90º,∠A=30º.求证:BC=AB.21D这个结论从直角三角形的性质定理2推出来21BC=AB21CD=AB21BD=AB逆命题:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30º.已知:如图,在Rt△ABC中,∠ACB=90º,BC=AB.求证:∠A=30º.21D分析做斜边AB上的中线CD,构造出等边△BCD得∠B=60º,从而得∠A=30º.是真命题吗?是真命题60º30°30°60°需证AD=BD,从而BD=CD.21Rt△ADC中,∠C=30º得AD=CD.21AB=AC,∠B=30º,可得到∠C=30º.分析证明:例题3已知:如图,在△ABC中,AB=AC,∠B=30º,AD⊥AC.求证:BD=CD.21变式2:E已知:如图,在△ABC中,AB=AC,∠BAC=120º,AB边上的垂直平分线交BC于点D,交AB于点E.求证:BD=CD.21D变式1已知:如图,在△ABC中AB=AC,AD=CD,AD⊥AC.求∠BAC的度数.21例题4已知:如图,在Rt△ABC中,∠ACB=90º,CD⊥AB,点D为垂足,CE是斜边AB边上的中线,且ED=BD.求证:∠A=30º.ABCB21根据推论2得:∠A=30º例题4如图,在Rt△ABC中,∠ACB=90º,CD⊥AB,点D为垂足,CE是斜边AB边上的中线,且ED=BD.求证:∠A=30º.证明:例题4已知:如图,在Rt△ABC中,∠ACB=90º,CD⊥AB,点D为垂足,CE是斜边AB边上的中线,且ED=BD.求证:∠A=30º.变式已知:如图,在Rt△ABC中,∠ACB=90º,∠A=30º,CE是斜边AB边上的中线,且ED=BD.求证:CD⊥AB.30º图中,与CE相等的线段有哪些?点D是线段AB的几等分点?如图,已知,AP平分PM//AB,AM=5,,求PD的长.,30BACABPD课本P120/4BAC如图,已知∠POQ=90º,你能不用量角器在图中画出一个直角三角形,使这个三角形以∠POQ为它的一个内角,并且有一个锐角为30º吗?OPQ推论1:在直角三角形中,如果有一个锐角等于30º,那么它所对的直角边等于斜边的一半.21a2a30°推论2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30º.21a2a30°练习册习题19.8(2)