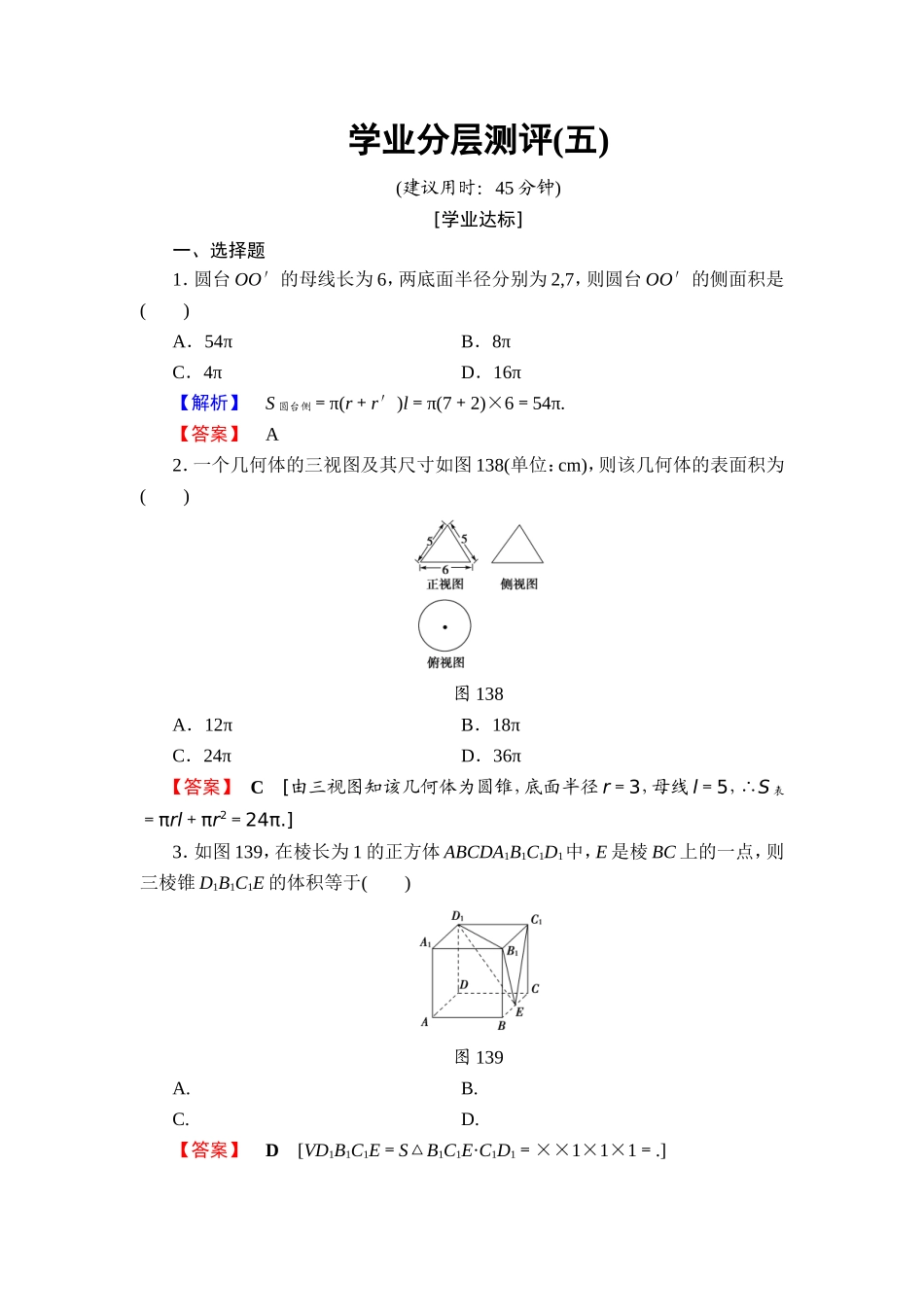
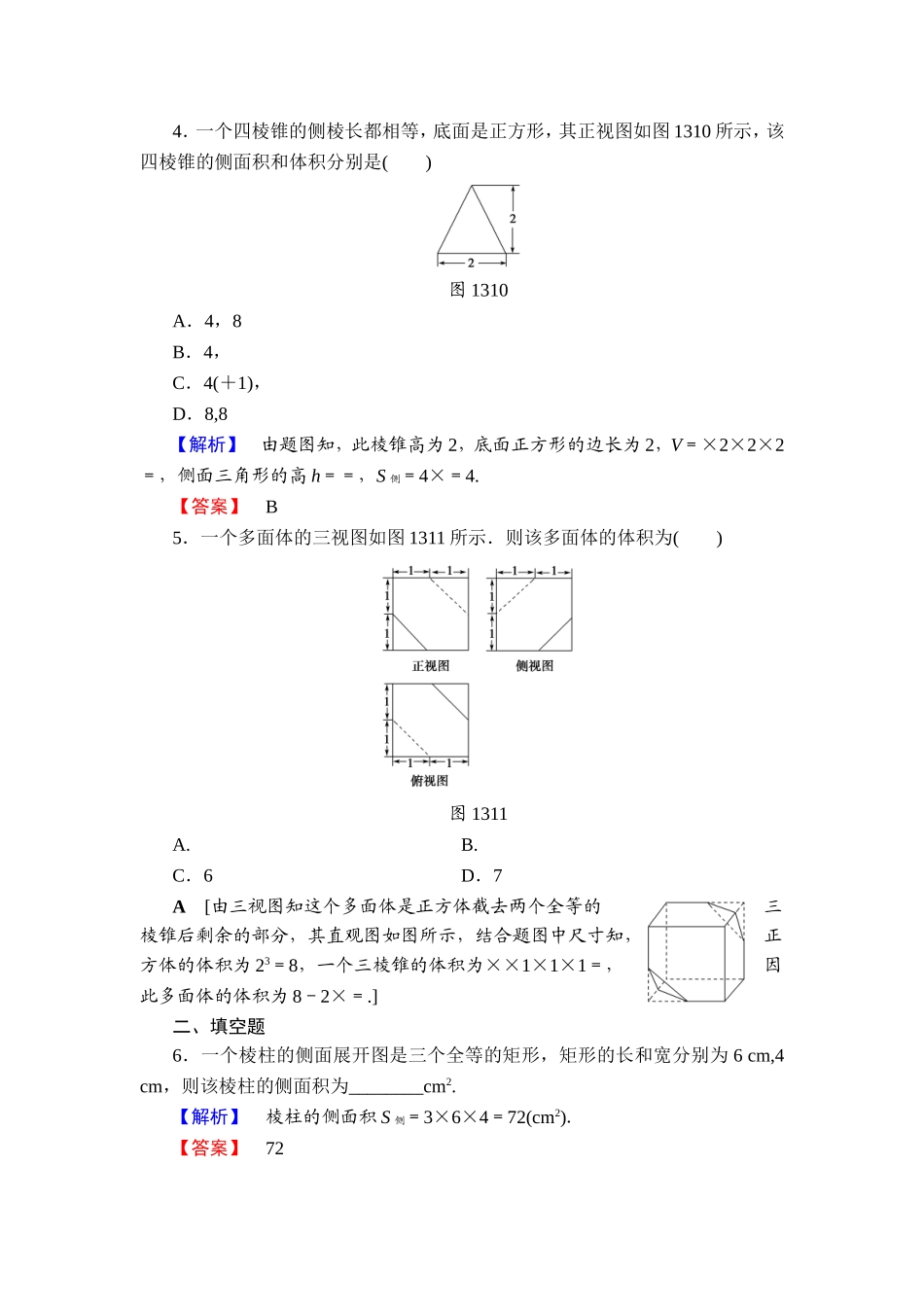
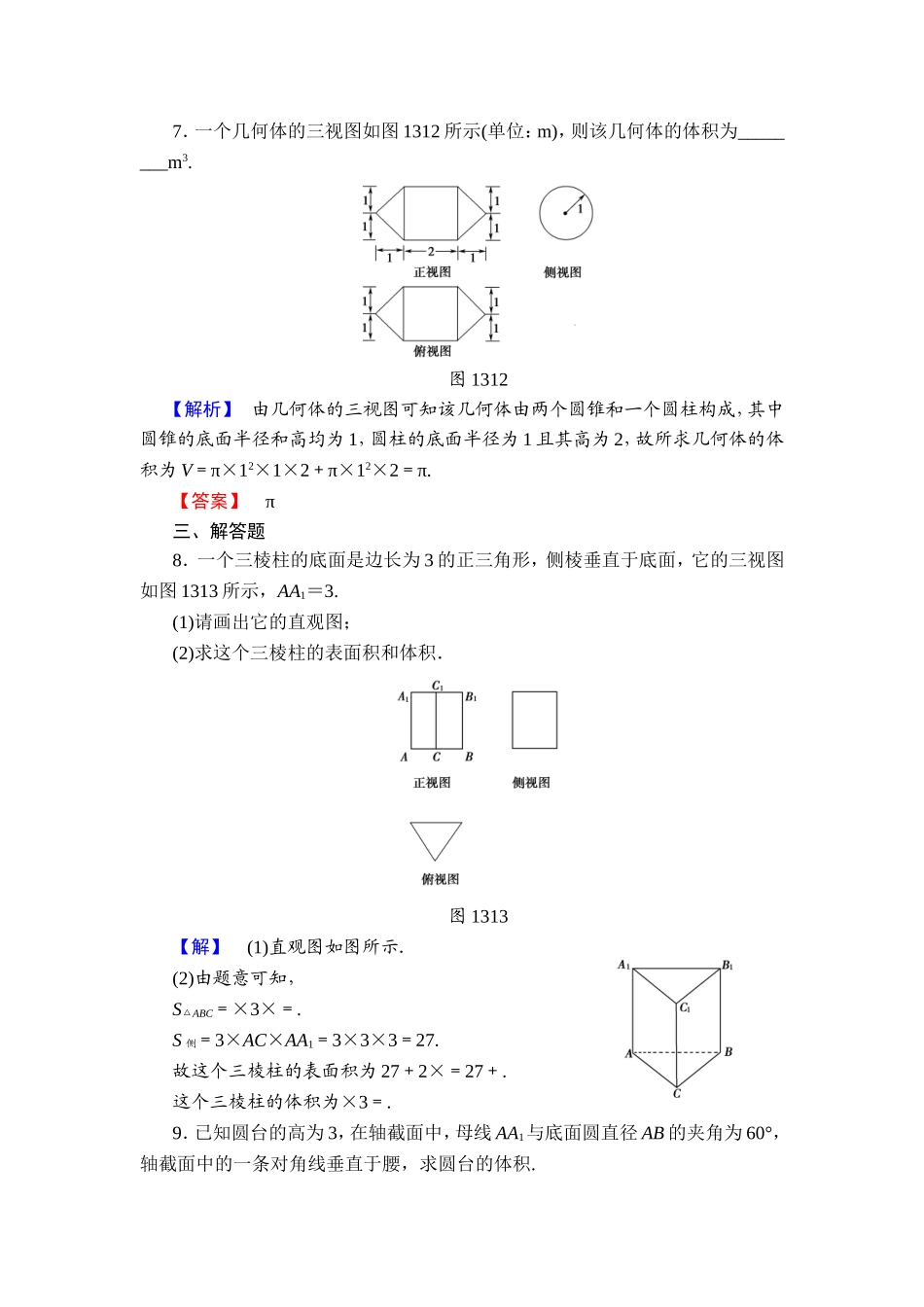
学业分层测评(五)(建议用时:45分钟)[学业达标]一、选择题1.圆台OO′的母线长为6,两底面半径分别为2,7,则圆台OO′的侧面积是()A.54πB.8πC.4πD.16π【解析】S圆台侧=π(r+r′)l=π(7+2)×6=54π.【答案】A2.一个几何体的三视图及其尺寸如图138(单位:cm),则该几何体的表面积为()图138A.12πB.18πC.24πD.36π【答案】C[由三视图知该几何体为圆锥,底面半径r=3,母线l=5,∴S表=πrl+πr2=24π.]3.如图139,在棱长为1的正方体ABCDA1B1C1D1中,E是棱BC上的一点,则三棱锥D1B1C1E的体积等于()图139A.B.C.D.【答案】D[VD1B1C1E=S△B1C1E·C1D1=××1×1×1=.]4.一个四棱锥的侧棱长都相等,底面是正方形,其正视图如图1310所示,该四棱锥的侧面积和体积分别是()图1310A.4,8B.4,C.4(+1),D.8,8【解析】由题图知,此棱锥高为2,底面正方形的边长为2,V=×2×2×2=,侧面三角形的高h==,S侧=4×=4.【答案】B5.一个多面体的三视图如图1311所示.则该多面体的体积为()图1311A.B.C.6D.7A[由三视图知这个多面体是正方体截去两个全等的三棱锥后剩余的部分,其直观图如图所示,结合题图中尺寸知,正方体的体积为23=8,一个三棱锥的体积为××1×1×1=,因此多面体的体积为8-2×=.]二、填空题6.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6cm,4cm,则该棱柱的侧面积为________cm2.【解析】棱柱的侧面积S侧=3×6×4=72(cm2).【答案】727.一个几何体的三视图如图1312所示(单位:m),则该几何体的体积为________m3.图1312【解析】由几何体的三视图可知该几何体由两个圆锥和一个圆柱构成,其中圆锥的底面半径和高均为1,圆柱的底面半径为1且其高为2,故所求几何体的体积为V=π×12×1×2+π×12×2=π.【答案】π三、解答题8.一个三棱柱的底面是边长为3的正三角形,侧棱垂直于底面,它的三视图如图1313所示,AA1=3.(1)请画出它的直观图;(2)求这个三棱柱的表面积和体积.图1313【解】(1)直观图如图所示.(2)由题意可知,S△ABC=×3×=.S侧=3×AC×AA1=3×3×3=27.故这个三棱柱的表面积为27+2×=27+.这个三棱柱的体积为×3=.9.已知圆台的高为3,在轴截面中,母线AA1与底面圆直径AB的夹角为60°,轴截面中的一条对角线垂直于腰,求圆台的体积.【解】如图所示,作轴截面A1ABB1,设圆台的上、下底面半径和母线长分别为r、R,l,高为h.作A1D⊥AB于点D,则A1D=3.又 ∠A1AB=60°,...