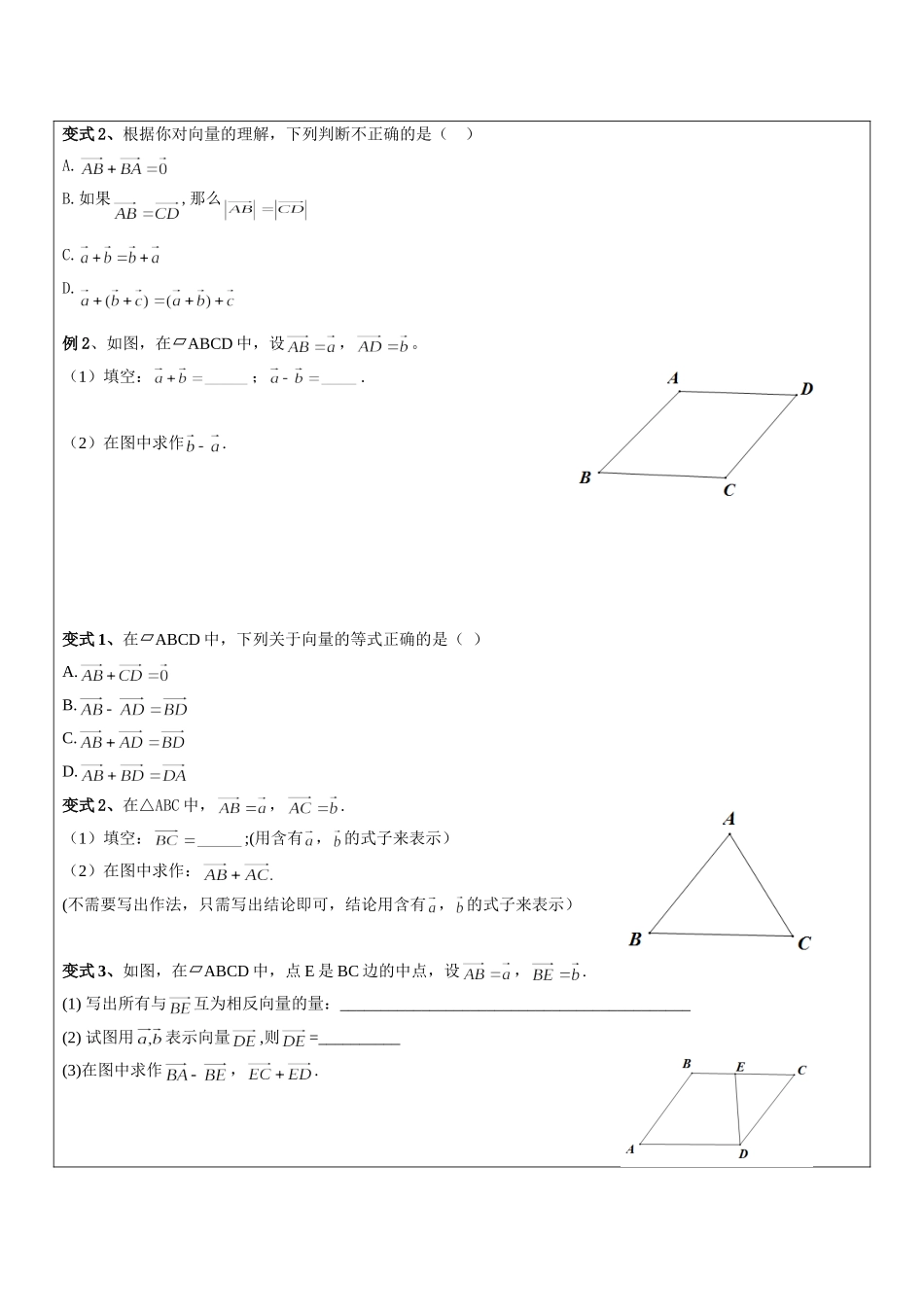
课题平面向量及其加减法教学目标1、熟悉平面向量的定义及其意义;2、熟悉掌握平面向量所遵守的三角形以及平行四边形法则;3、学会根据平面向量用某些向量的大小关系去表示其他的有向线段。重点、难点4、熟悉掌握平面向量所遵守的三角形以及平行四边形法则;5、学会根据平面向量用某些向量的大小关系去表示其他的有向线段教学内容一、【知识点梳理】(1)向量:既有又有的量叫做向量。向量的大小也叫做向量的(或者向量的);(2)相等的向量:的两个向量叫做相等的向量;(3)互为相反向量:的两个向量叫做互为相反向量;(4)平行向量:的两个向量叫做平行向量;(5)零向量:的向量叫做零向量;(6)向量的加法满足;(7)向量减法的三角形法则:;(8)向量加法的平行四边形法则:;二、【经典范例】例1、下列说法中不正确的是()A.零向量是没有方向的向量B.零向量的方向是任意的C.零向量与任意向量都平行D.零向量只能与零向量相等变式1、的负向量是()A.与方向相反的向量B.与符号相反的向量C.与反向且大小相等的向量D.以上均不对变式2、根据你对向量的理解,下列判断不正确的是()A.B.如果,那么C.D.例2、如图,在ABCD中,设,。(1)填空:;.(2)在图中求作.变式1、在ABCD中,下列关于向量的等式正确的是()A.B.C.D.变式2、在△ABC中,,.(1)填空:;(用含有,的式子来表示)(2)在图中求作:(不需要写出作法,只需写出结论即可,结论用含有,的式子来表示)变式3、如图,在ABCD中,点E是BC边的中点,设,.(1)写出所有与互为相反向量的量:___________________________________________(2)试图用表示向量,则=__________(3)在图中求作,.三、【课堂练习】1.两个非零向量,互为相反向量,那么下列各式正确的个数是()①.②.③.④.(A).1个(B).2个(C).3个(D).4个2.化简:_________3.如图,多边形ABCDEF是正六边形,设,.(1)试用向量,表示向量.(2)在图中求作:.(不要求写出作法,只需写出结论即可)4、如图,在梯形ABCD中,BC∥AD,设,..(1)填空:___(填“=”或者“≠”);(2)填空:_______(用,,的式子表示);(3)在图中求作.(不要求写出作法,只需写出结论即可,结论用,,的式子表示)四、【家庭作业】1、在梯形ABCD中,AD∥BC,过D作DE∥AC交BC的延长线于E,在图中指出下列几个向量的和.(1)(2)(3)(4).3、如图,P是线段AB的分点,且,下列各式正确的是(B)A.B.C.D.签字确认学员教师班主任