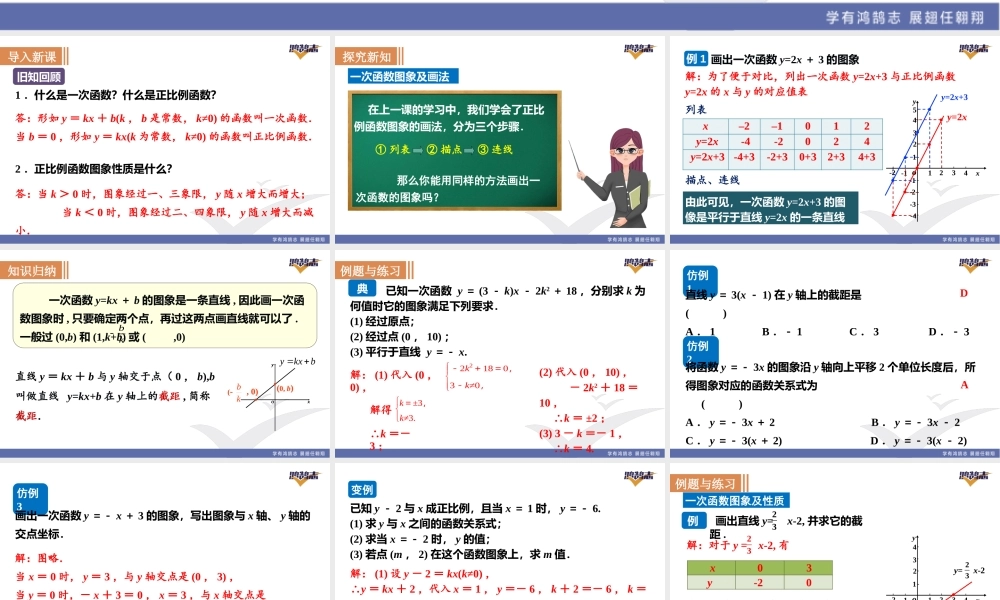
第十二章一次函数12.2一次函数第2课时一次函数的图象和性质旧知回顾导入新课1.什么是一次函数?什么是正比例函数?2.正比例函数图象性质是什么?答:形如y=kx+b(k,b是常数,k≠0)的函数叫一次函数.当b=0,形如y=kx(k为常数,k≠0)的函数叫正比例函数.答:当k>0时,图象经过一、三象限,y随x增大而增大;当k<0时,图象经过二、四象限,y随x增大而减小.探究新知在上一课的学习中,我们学会了正比例函数图象的画法,分为三个步骤.①列表②描点③连线那么你能用同样的方法画出一次函数的图象吗?一次函数图象及画法描点、连线列表x–2–1012y=2x-4-2024y=2x+3-4+3-2+30+32+34+3例1解:为了便于对比,列出一次函数y=2x+3与正比例函数y=2x的x与y的对应值表由此可见,一次函数y=2x+3的图像是平行于直线y=2x的一条直线画出一次函数y=2x+3的图象1234x-1-2o1234-1-2-35-4yy=2xy=2x+3一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或(,0)bkyxOyxObkxy(0,b)(,0)kb直线y=kx+b与y轴交于点(0,b),b叫做直线y=kx+b在y轴上的截距,简称截距.知识归纳典例例题与练习已知一次函数y=(3-k)x-2k2+18,分别求k为何值时它的图象满足下列要求.(1)经过原点;(2)经过点(0,10);(3)平行于直线y=-x.(2)代入(0,10),-2k2+18=10,∴k=±2;(3)3-k=-1,∴k=4.解:(1)代入(0,0),,-2k2+18=0,3-k≠0,解得k=±3,k≠3.+18=0,≠0,解得k=±3,k≠3.解得∴k=-3;仿例1直线y=3(x-1)在y轴上的截距是()A.1B.-1C.3D.-3仿例2将函数y=-3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为()A.y=-3x+2B.y=-3x-2C.y=-3(x+2)D.y=-3(x-2)DA仿例3画出一次函数y=-x+3的图象,写出图象与x轴、y轴的交点坐标.解:图略.当x=0时,y=3,与y轴交点是(0,3),当y=0时,-x+3=0,x=3,与x轴交点是(3,0).变例已知y-2与x成正比例,且当x=1时,y=-6.(1)求y与x之间的函数关系式;(2)求当x=-2时,y的值;(3)若点(m,2)在这个函数图象上,求m值.解:(1)设y-2=kx(k≠0),∴y=kx+2,代入x=1,y=-6,k+2=-6,k=-8,∴y=-8x+2;(2)当x=-2时,y=18;(3)代入(m,2),-8m+2=2,m=0.一次函数图象及性质例3解:对于y=x-2,有23过两点(0,-2),(3,0)画直线,即得y=x-2的图象....