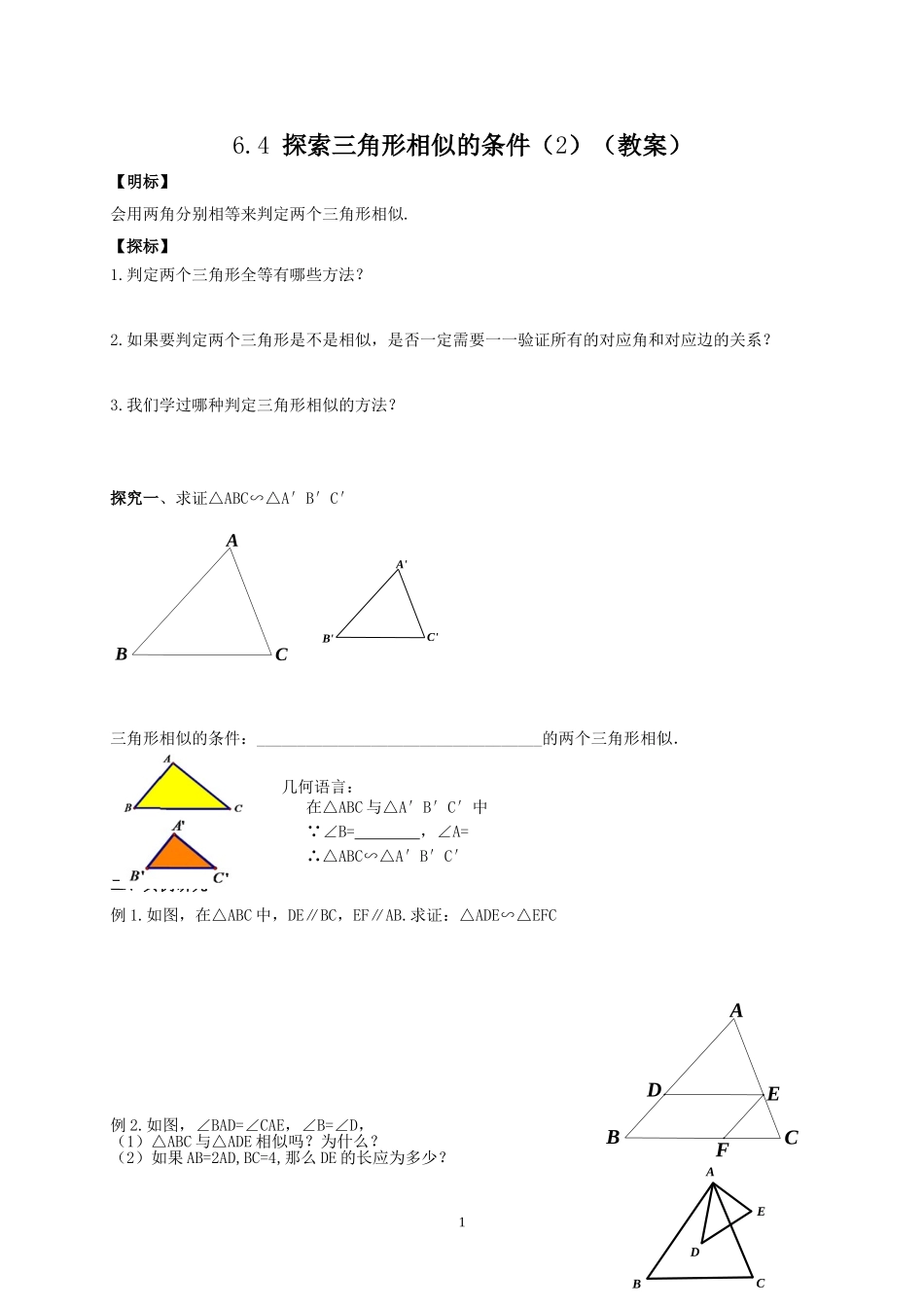
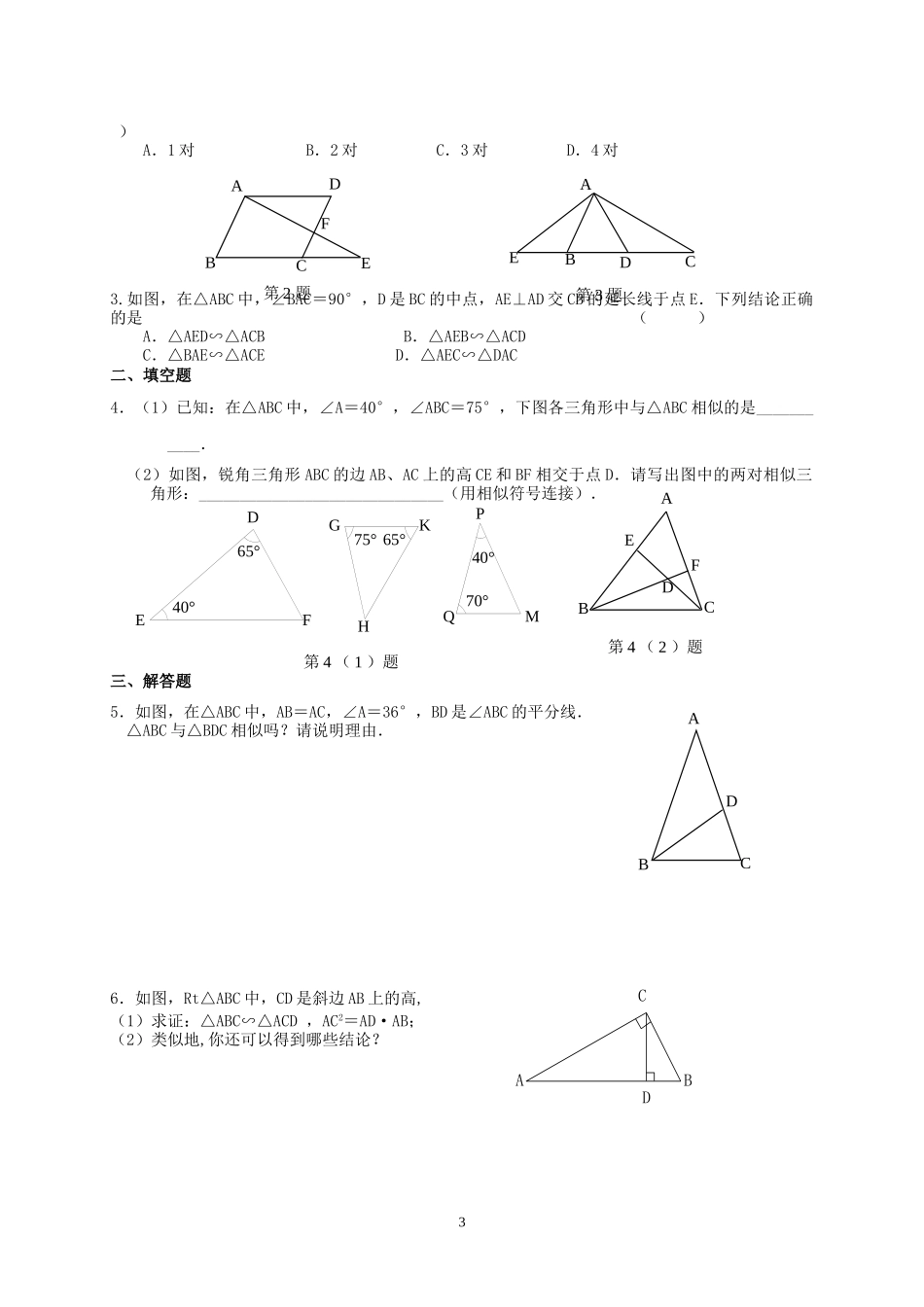
B'A'C'BACDFE6.4探索三角形相似的条件(2)(教案)【明标】会用两角分别相等来判定两个三角形相似.【探标】1.判定两个三角形全等有哪些方法?2.如果要判定两个三角形是不是相似,是否一定需要一一验证所有的对应角和对应边的关系?3.我们学过哪种判定三角形相似的方法?探究一、求证△ABC∽△A′B′C′BAC三角形相似的条件:___________________________________的两个三角形相似.几何语言:在△ABC与△A′B′C′中 ∠B=,∠A=∴△ABC∽△A′B′C′二、典例研究例1.如图,在△ABC中,DE∥BC,EF∥AB.求证:△ADE∽△EFC例2.如图,∠BAD=∠CAE,∠B=∠D,(1)△ABC与△ADE相似吗?为什么?(2)如果AB=2AD,BC=4,那么DE的长应为多少?1CBADEBACD例3.如图,在矩形ABCD中,点EF、分别在边ADDC、上,若BE⊥EF,求证:ABEDEF△∽△.【达标】1.判断下列说法是否正确?并说明理由.(1)所有的等腰三角形都相似.()(2)所有的等腰直角三角形都相似.()(3)所有的等边三角形都相似.()(4)所有的直角三角形都相似.()(5)有一个角是100°的两个等腰三角形都相似.()(6)有一个角是70°的两个等腰三角形都相似.()2.如图,在△ABC中BD⊥AC,AE⊥BC,图中一定和△BDC相似的三角形有几个?它们分别是哪些三角形?3.如图,在△ABC中,D是AB边上一点,且∠ACD=∠B求证:(1)△ACD∽△ABC(2)AC2=ADAB6.4探索三角形相似的条件(2)(学案)一、选择题1.具备下列各组条件的两个三角形中,不一定相似的是()A.有一个角是40°的两个等腰三角形B.两个等腰直角三角形C.有一个角为100°的两个等腰三角形D.两个等边三角形2.如图,在□ABCD中,点E在边BC的延长线上,连接AE交CD于点F.图中的相似三角形有(2OBACDE)A.1对B.2对C.3对D.4对3.如图,在△ABC中,∠BAC=90°,D是BC的中点,AE⊥AD交CB的延长线于点E.下列结论正确的是()A.△AED∽△ACBB.△AEB∽△ACDC.△BAE∽△ACED.△AEC∽△DAC二、填空题4.(1)已知:在△ABC中,∠A=40°,∠ABC=75°,下图各三角形中与△ABC相似的是___________.(2)如图,锐角三角形ABC的边AB、AC上的高CE和BF相交于点D.请写出图中的两对相似三角形:______________________________(用相似符号连接).三、解答题5.如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的平分线.△ABC与△BDC相似吗?请说明理由.6.如图,Rt△ABC中,CD是斜边AB上的高,(1)求证:△ABC∽△ACD,AC2=AD·AB;(2)类...