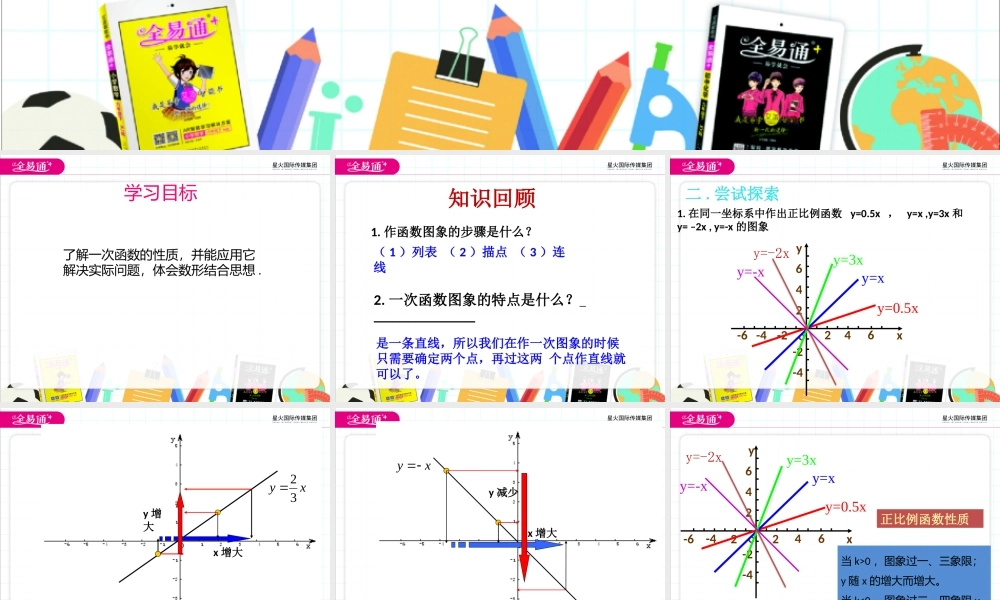
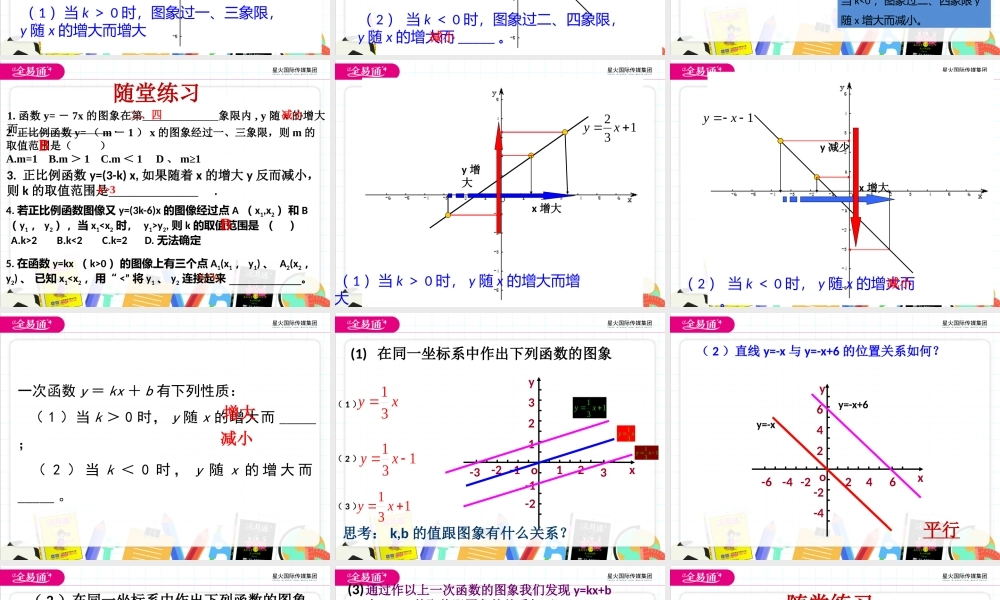
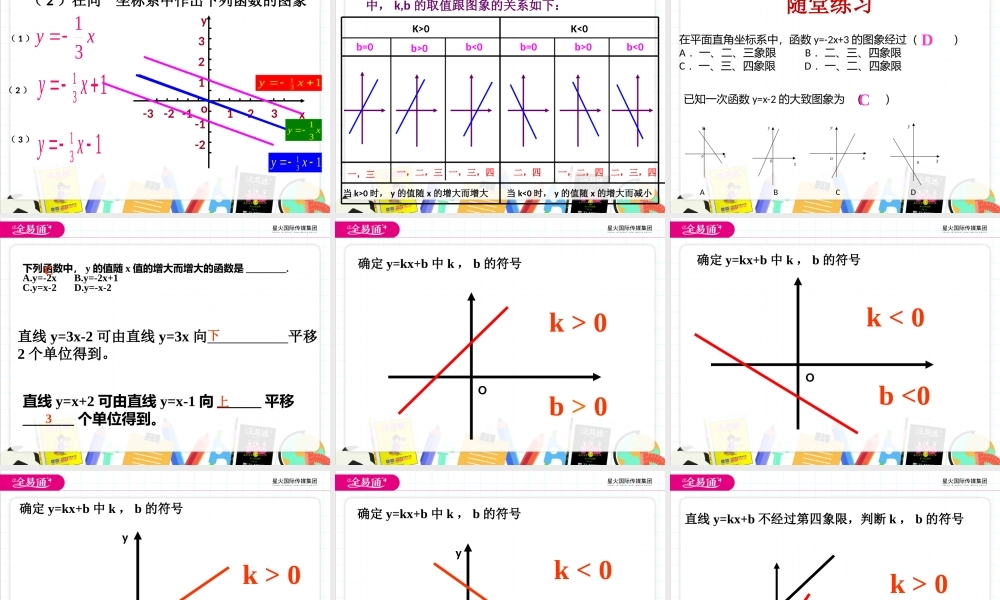
10.3一次函数的性质学习目标了解一次函数的性质,并能应用它解决实际问题,体会数形结合思想.1.作函数图象的步骤是什么?(1)列表(2)描点(3)连线2.一次函数图象的特点是什么?是一条直线,所以我们在作一次图象的时候只需要确定两个点,再过这两个点作直线就可以了。知识回顾二.尝试探索1.在同一坐标系中作出正比例函数y=0.5x,y=x,y=3x和y=–2x,y=-x的图象-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2xy=-xxy32x增大y增大(1)当k>0时,图象过一、三象限,y随x的增大而增大xyx增大y减少(2)当k<0时,图象过二、四象限,y随x的增大而_____。减小-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2x正比例函数性质当k>0,图象过一、三象限;y随x的增大而增大。当k<0,图象过二、四象限y随x增大而减小。y=-x2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是()A.m=1B.m>1C.m<1D、m≥1B1.函数y=-7x的图象在第象限内,y随x的增大而.二、四减小3.正比例函数y=(3-k)x,如果随着x的增大y反而减小,则k的取值范围是.k>34.若正比例函数图像又y=(3k-6)x的图像经过点A(x1,x2)和B(y1,y2),当x1y2,则k的取值范围是()A.k>2B.k<2C.k=2D.无法确定5.在函数y=kx(k>0)的图像上有三个点A1(x1,y1)、A2(x2,y2)、已知x10b=0b>0b<0b=0b>0b<0通过作以上一次函数的图象我们发现y=kx+b中,k,b的取值跟图象的关系如下:K<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小(3)在平面直角坐标系中,函数y=-2x+3的图象经过()A.一、二、三象限B.二、三、四象限C.一、三、四象限D.一、二、四象限已知一次函数y=x-2的大致图象为...