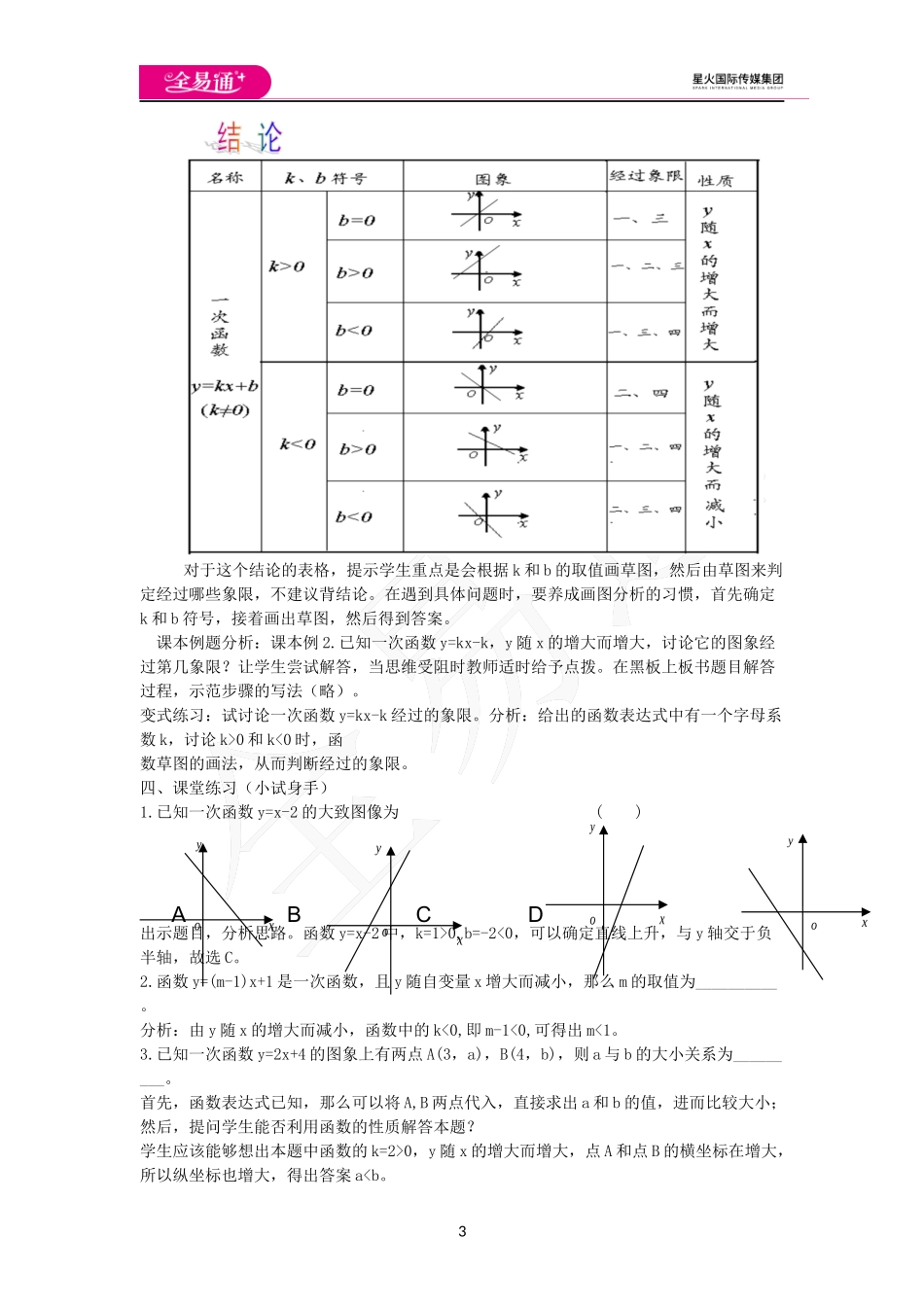
110.3一次函数的性质教学目标【知识与能力】(1)根据一次函数y=kx+b的表达式和图象,探索并理解k>0和k<0时,函数图象的变化情况。(2)理解一次函数表达式中系数k和b的值对函数性质的影响。【过程与方法】(1)通过动手画一次函数图象,经历探索一次函数图像性质的过程,初步体验借助图像研究函数性质的方法。(2)经历由一次函数图象探索其性质的过程,培养学生观察、分析、归纳、概括的能力。【情感态度价值观】(1)在探索一次函数的过程中,体会数形结合、转化、分类讨论等数学思想,体会函数图象在研究函数性质时的重要作用。(2)在小组合作中,培养学生与他人交流的能力和分享、合作精神。教学重难点【教学重点】一次函数性质的理解和应用。【教学难点】一次函数性质的探索过程及性质的理解和应用。课前准备无教学过程一、课前自主探究上课的前一天布置预习作业,自主完成预习学案。主要是画出函数y=x-1和y=3x+1,y=2x的图象,自主归纳当k>0时的函数性质;画出y=-x-1和y=-3x+1,y=-2x的图象,进而归纳系数k对函数性质的影响。学生结合微课,进行自学,熟悉函数图象的画法,为课堂学习打好基础。二、复习导入1.一次函数的概念是什么?一次函数的图象是什么形状?已知一次函数y=kx+b(k≠0),如何画出函数图象?一次函数图象与坐标轴交点坐标是什么?求法是怎样的?采用一问一答的方式引导学生回答问题,一次函数的图象是一条直线,画函数图象只需取两个点,为了简便一般取点(0,b)和(−bk,0)。提示学生回忆直线与坐标轴交点的求法。三、重点知识讲解重点知识1:系数k>0,和k<0时,函数图像的变化情况2首先,课件出示学生画的函数y=x-1和y=3x+1,y=2x的图象,学生通过自学可以总结出k>0,函数图象的形式是上升的;同样地,课件出示函数y=-x-1和y=-3x+1,y=-2x的图象,学生很熟练地说出,当k<0时,函数图象是下降的。利用课件展示教材图10-9(类似一次函数y=2x+4,k>0的函数图象)。在直线上取一动点P,演示该点沿直线从左下方向右上方运动的情况,分别将这个点的横、纵坐标也用不同颜色点表示。让学生发现点横、纵坐标发生怎样的变化,这说明当自变量x逐渐增大时,函数值y发生怎样的变化?此时学生能够归纳出当横坐标逐渐增大时,点的纵坐标也逐渐增大。这说明,当k>0时,图象上升,y随x的增大而增大。同样的过程,引导学生归纳:当k<0时,图象上升,y随x的增大而减小。这样学生得出了本节的第一个重点知识:对于一次函数y=kx+b,当k>0时,y随x...