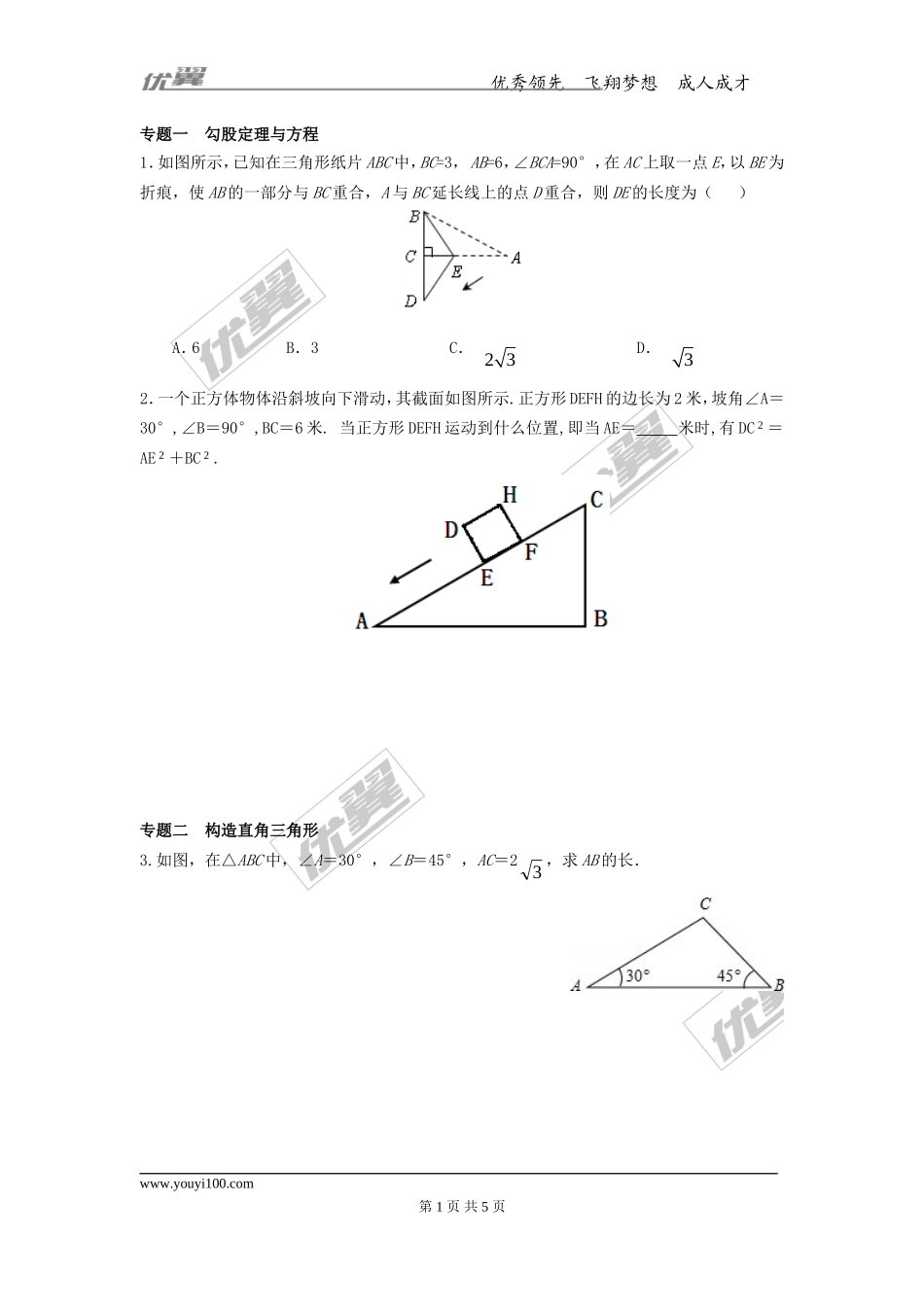
优秀领先飞翔梦想成人成才专题一勾股定理与方程1.如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为()A.6B.3C.23D.32.一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=米时,有DC2=AE2+BC2.专题二构造直角三角形3.如图,在△ABC中,∠A=30°,∠B=45°,AC=23,求AB的长.www.youyi100.com第1页共5页优秀领先飞翔梦想成人成才4.如图,在四边形ABCD中,AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,求∠DAB的度数.专题三勾股定理中的分类讨论思想5.在等腰△ABC中,∠A=30°,AB=8,则AB边上的高CD的长是.6.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为_______.7.在△ABC中,AB=25,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.参考答案www.youyi100.com第2页共5页优秀领先飞翔梦想成人成才1.C解析:由折叠可知BC=BA=6,DE=AE, BC=3,∴CD=BC=3,∴BE=DE=AE,由勾股定理可得AC=33,设DE=AE=BE=x,在Rt△BCE中,32+233x=x2,解得x=23,即DE的长度为23.2.143解析:因为∠A=30°,∠B=90°,BC=6米,所以AC=12米.设当AE为x时,所以EC=12-x,由DC2=AE2+BC2及DC2=DE2+EC2,所以有22+(12-x)2=x2+36,解得x=143.3.解:过C作CD⊥AB于D,∴∠ADC=∠BDC=90°, ∠B=45°,∴∠BCD=∠B=45°,∴CD=BD. ∠A=30°,AC=23,∴CD=3,∴BD=CD=3,由勾股定理得:AD=22ACCD=3,∴AB=AD+BD=3+3.答:AB的长是3+3.4.解:连结AC.设AB、BC、CD、DA分别为2x,2x,3x,x,则2222228,,9ACxADxCDx,∴222ACADCD,∴∠DAC=90°,∴∠DAB=90°+45°=135°.www.youyi100.com第3页共5页优秀领先飞翔梦想成人成才5.433或43或4解析:(1)如图①,当AB=AC时, ∠A=30°,∴CD=12AC=12×8=4;(2)如图②,当AB=BC时,则∠A=∠ACB=30°,∴∠ACD=60°,∴∠BCD=30°,∴BD=1=42BC,∴CD=22BCBD=43;(3)如图③,当AC=BC时,则AD=4,设CD=x,则AC=2x.则2222)4xx(,解得x=433.故答案为:433或43或4.6.42或32解析:当△ABC是锐角三角形时,如图①,根据勾股定理可得BD=9,DC=5,∴BC=14,此时△ABC的周长为15+13+14=42;当△ABC是钝角三角形时,如图②,根据勾股定理可...