北京课改初中数学八下《16.4特殊的平行四边形的性质与判定》PPT课件.pptVIP免费

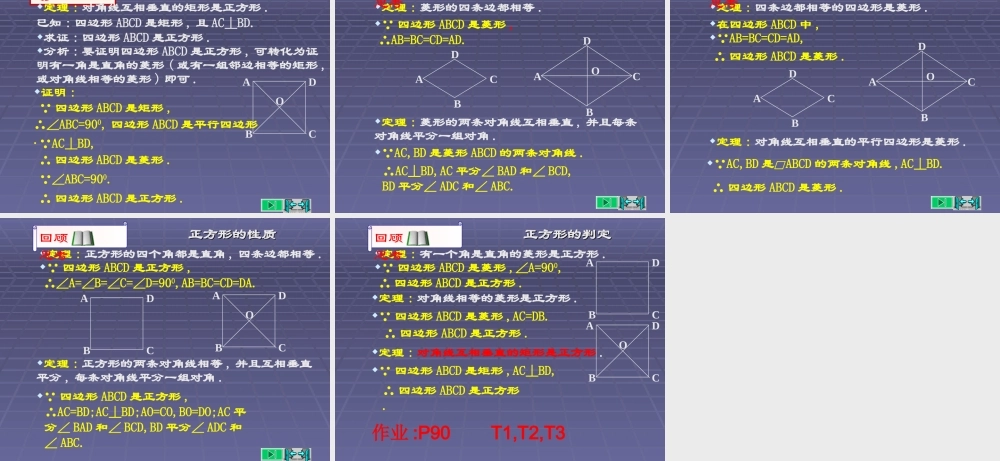
2.2.特殊的平行四边形特殊的平行四边形(2)(2)菱形菱形,,正方形的性质及判定正方形的性质及判定四边形之间的关系四边形之间的关系我思,我进步11四边形之间有何关系？特殊的平行四边形之间呢？还记得它们与平行四边形的关系吗?能用一张图来表示它们之间的关系吗?四边形平行四边形矩形菱形正方形两组对边分别平行有一个角是直角有一组邻边相等有一个角是直角有一组邻边相等一组对边平行另一组对边不平行梯形两腰相等等腰梯形腰与底垂直直角梯形矩形的性质矩形的性质,,推论推论定理:矩形的四个角都是直角.定理:矩形的两条对角线相等.推论(直角三角形性质):直角三角形斜边上的中线等于斜边的一半.回顾思考DBCADBCAABCD矩形的判定矩形的判定,,直角三角形直角三角形的判定的判定定理:有三个角是直角的四边形是矩形.定理:对角线相等的平行四边形是矩形.定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.回顾思考DBCADBCAABCD菱形的性质菱形的性质定理:菱形的四条边都相等.我思,我进步22已知:如图,四边形ABCD是菱形.分析:由菱形的定义,利用平行四边形性质可使问题得证.证明: 四边形ABCD是菱形,∴AB=AD,四边形ABCD是平行四边形.∴AB=CD,AD=BC.求证:AB=BC=CD=DA.∴AB=BC=CD=AD.CBDA菱形的性质菱形的性质我思,我进步33定理:菱形的两条对角线互相垂直,并且每条对角线平分一组对角.已知:如图,AC,BD是菱形ABCD的两条对角线,AC,BD相交于点O.求证:(1).AC⊥BD;(2).AC平分∠BAD和∠BCD,BD平分∠ADC和∠ABC.证明:(1) 四边形ABCD是菱形,∴AD=CD,AO=CO.又 DO=DO,∴△AOD≌△COD(SSS).∴∠AOD=∠COD=900.DBCAO∴AC⊥BD.(2) AD=AB,DA=DC,AC⊥BD;∴AC平分∠BAD和∠BCD,BD平分∠ADC和∠ABC由此题的证明,你能得出菱形的面积与两对角线有何关系?菱形性质的应用菱形性质的应用例题欣赏44已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求:(1).对角线AC的长度;(2).菱形ABCD的面积.解:(1) 四边形ABCD是菱形,=2×△ABD的面积11105.22DEBDcm∴∠AED=900,(2)菱形ABCD的面积=△ABD的面积+△CBD的面积222213512.AEADDEcm∴AC=2AE=2×12=24(cm).122BDAEDBCAE2121012120.2cm菱形的判定菱形的判定定理:四条边都相等的四边形是菱形.我思,我进步22已知:如图,在四边形ABCD中,AB=BC=CD=DA..分析:利用菱形定义和两组对边分别相等的四边形是平行四边形,可使问...