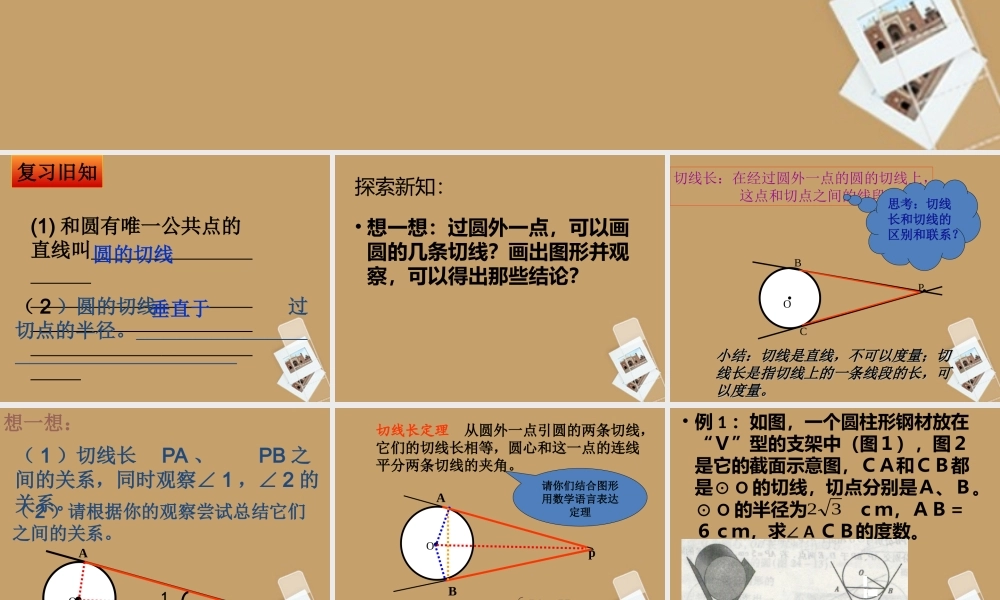
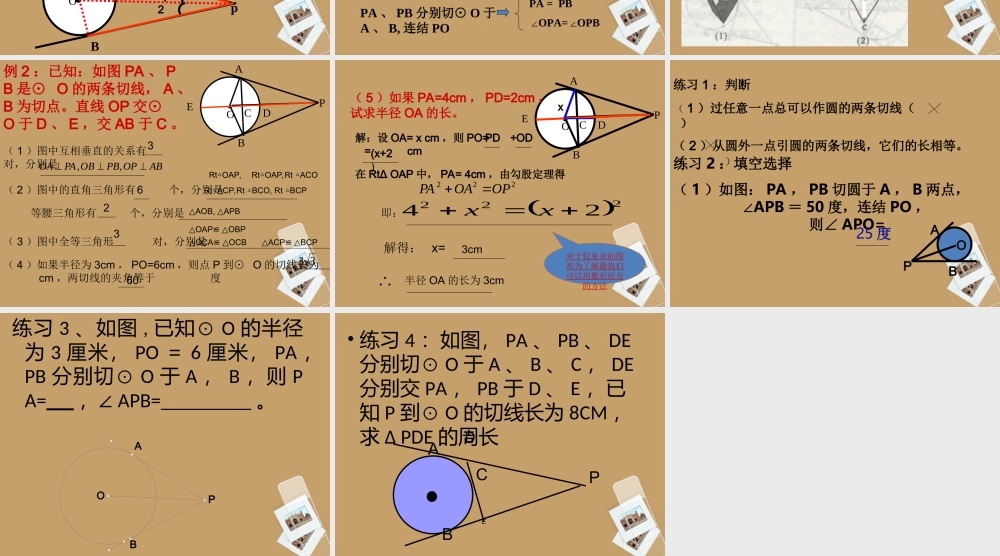
(1)和圆有唯一公共点的直线叫(2)圆的切线过切点的半径。圆的切线垂直于复习旧知探索新知:•想一想:过圆外一点,可以画圆的几条切线?画出图形并观察,可以得出那些结论?PBCO切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。思考:切线长和切线的区别和联系?小结:切线是直线,不可以度量;切小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可线长是指切线上的一条线段的长,可以度量。以度量。想一想:pABO12(2)请根据你的观察尝试总结它们之间的关系。(1)切线长PA、PB之间的关系,同时观察∠1,∠2的关系。切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO请你们结合图形用数学语言表达定理PA、PB分别切⊙O于A、B,连结POPA=PB∠OPA=OPB∠•例1:如图,一个圆柱形钢材放在“V”型的支架中(图1),图2是它的截面示意图,CA和CB都是⊙O的切线,切点分别是A、B。⊙O的半径为cm,AB=6cm,求∠ACB的度数。32例2:已知:如图PA、PB是⊙O的两条切线,A、B为切点。直线OP交⊙O于D、E,交AB于C。OPABCDE(1)图中互相垂直的关系有对,分别是(2)图中的直角三角形有个,分别是等腰三角形有个,分别是(3)图中全等三角形对,分别是(4)如果半径为3cm,PO=6cm,则点P到⊙O的切线长为cm,两切线的夹角等于度3ABOPPBOBPAOA,,6233360RtOAP,△RtOAP,RtACO△△RtACP,RtBCO,RtBCP△△△△AOB,APB△△OAPOBP≌△△OCAOCB≌△△ACPBCP≌△OPABCDE(5)如果PA=4cm,PD=2cm,试求半径OA的长。x解:设OA=xcm,则PO=+=cm在RtΔOAP中,PA=4cm,由勾股定理得222OPOAPA即:解得:x=对于较复杂的图形为了解题我们可以用数形结合的方法PDOD(x+2)22224xx3cm半径OA的长为3cm练习1:判断(1)过任意一点总可以作圆的两条切线()(2)从圆外一点引圆的两条切线,它们的长相等。()PBOA练习2:填空选择(1)如图:PA,PB切圆于A,B两点,∠APB=50度,连结PO,则∠APO=25度练习3、如图,已知⊙O的半径为3厘米,PO=6厘米,PA,PB分别切⊙O于A,B,则PA=,∠APB=_________。OPBA•练习4:如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,求ΔPDE的周长DCBEPA