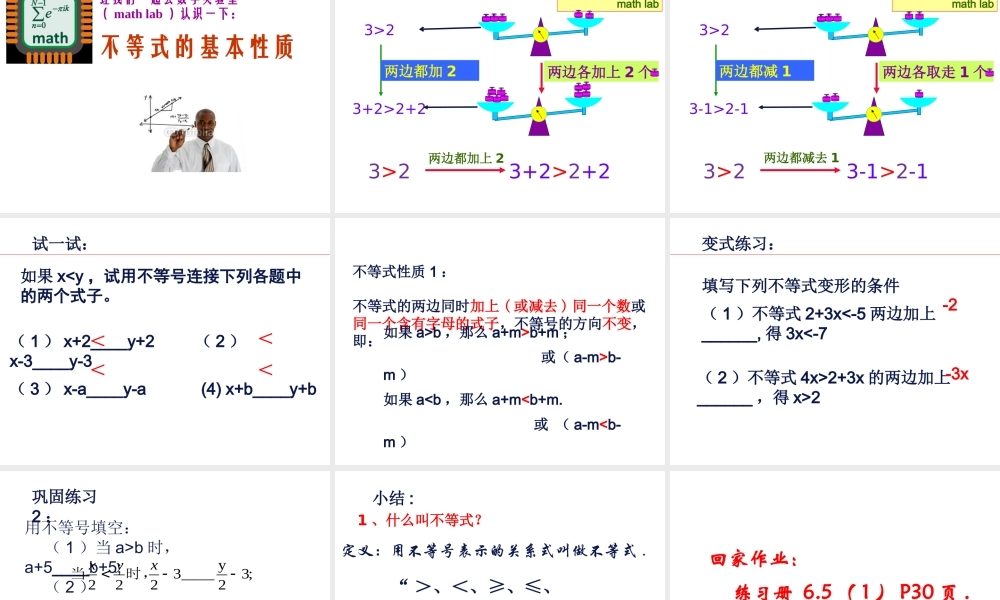
不等式及其性质(1)A.在大人的带领下,身高1.2米以下(不包括1.2米)的儿童乘公共汽车可以免买车票.(用h表示儿童的身高.)B.消费金额多于30元的顾客可以凭收银条参加抽奖活动.(其中M表示消费金额.)h<1.2(米)M>30(元)课前练习:列式表示下列题目的意义在实际生活中除了等量关系外,还存在着很多像上面这样的不等量关系!数学与生活今天,让我们一起走进不等式的世界里.4040你能用语言表述下面两个交通标志中的数字符号所表示的意义吗?4m汽车的速度不超过40km/h汽车的高度不超过4m速度v≤40(千米/小时)高度h≤4(米)思考1:温故什么是等式?定义:用等号“=”连接的式子叫做等式。知新什么是不等式?定义:用不等号连接的式子叫做不等式。“>、<、≥、≤、≠”≠——不等于——不等号>——大于<——小于≤——小于或等于≥——大于或等于不等号的含义:≤≥><≠试一试判断下列各式中哪些是不等式?(1)a2+1>0(2)a+b=0(3)8<9(4)3x-1≤x(5)4-2x(6)x-y≠1是不是是是不是是例1.用不等式表示(1)a与b的和小于0;(2)x的一半减去3所得的差大于或等于5.分析:(1)a与b的和小于0a+b<0(2)x的一半减去3大于或等于52x3≥5532x0ba巩固练习1:用不等式表示:(1)a与5的和大于-3;(2)某数的4倍小于或等于12;(3)某数的3倍减去2的差是一个非负数;(4)b的一半小于a与b的积。小游戏:请同学们模仿例题,列举不等式的例子,并点名请其他同学回答。关键词语不等号第一类——明显的不等关系比…大大于>小于<≤至多不大于不超过≥不小于不低于至少超过低于比…小注意“不”字哦!≠大于或小于不等于总结归纳:总结归纳:第二类——隐含的不等关系正数负数非负数非正数非零数>0<0≥0≤0≠0小结:①抓住关键词②选准不等号等式的基本性质1:等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,等式仍成立。思考2:不等式是否具有这些类似性质?不等式的基本性质让我们一起去数学实验室(mathlab)认识一下:数学实验室mathlab不等式3>2的变形过程:3>2两边都加23+2>2+2两边各加上2个3>23+2>2+2两边都加上2数学实验室mathlab不等式3>2的变形过程:3>2两边都减13-1>2-1两边各取走1个3>23-1>2-1两边都减去1如果xb,那么a+...