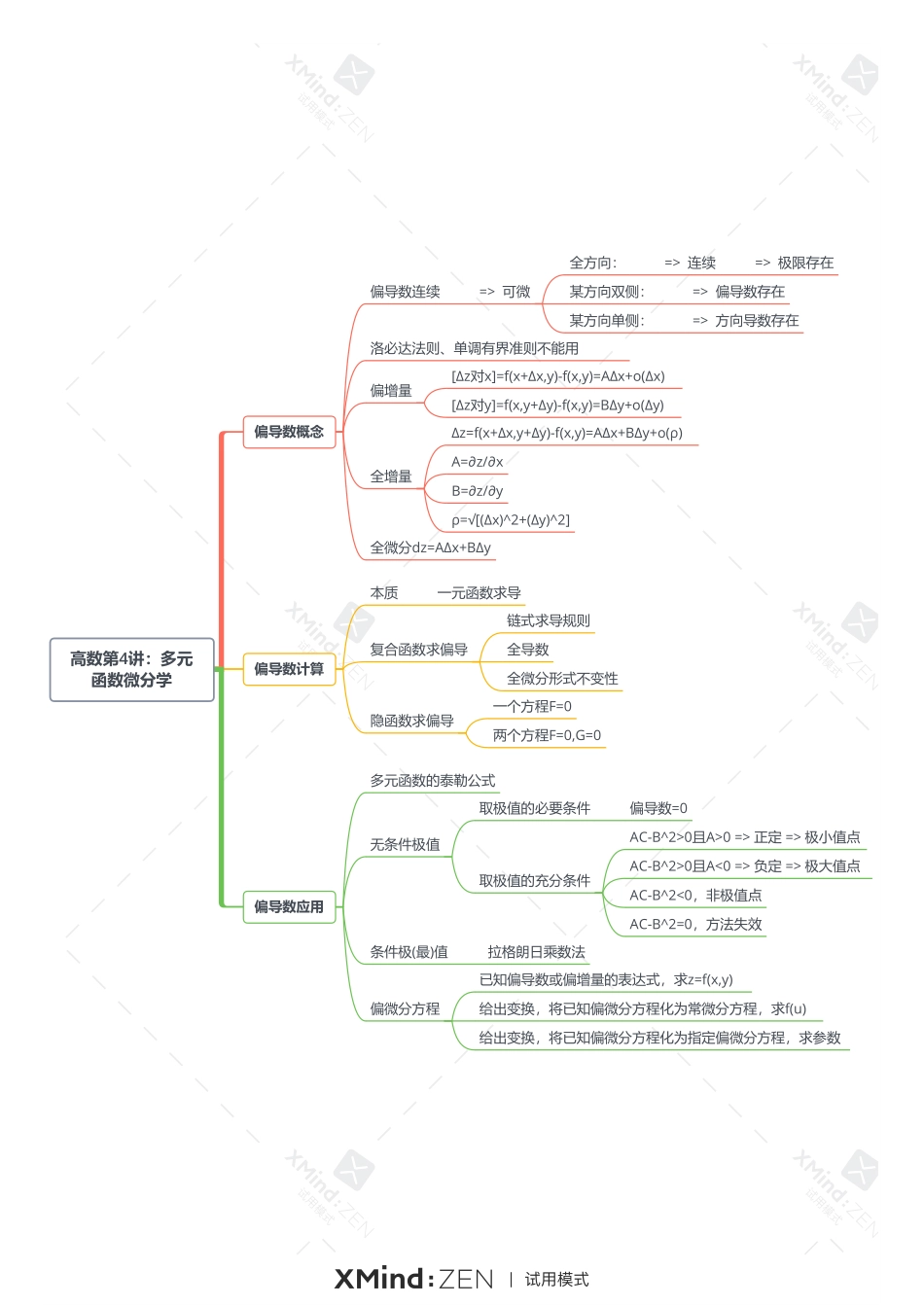
高数第4讲:多元函数微分学偏导数概念偏导数连续=>可微全方向:=>连续=>极限存在某方向双侧:=>偏导数存在某方向单侧:=>方向导数存在洛必达法则、单调有界准则不能用偏增量[Δz对x]=f(x+Δx,y)-f(x,y)=AΔx+o(Δx)[Δz对y]=f(x,y+Δy)-f(x,y)=BΔy+o(Δy)全增量Δz=f(x+Δx,y+Δy)-f(x,y)=AΔx+BΔy+o(ρ)A=∂z/∂xB=∂z/∂yρ=√[(Δx)^2+(Δy)^2]全微分dz=AΔx+BΔy偏导数计算本质一元函数求导复合函数求偏导链式求导规则全导数全微分形式不变性隐函数求偏导一个方程F=0两个方程F=0,G=0偏导数应用多元函数的泰勒公式无条件极值取极值的必要条件偏导数=0取极值的充分条件AC-B^2>0且A>0=>正定=>极小值点AC-B^2>0且A<0=>负定=>极大值点AC-B^2<0,非极值点AC-B^2=0,方法失效条件极(最)值拉格朗日乘数法偏微分方程已知偏导数或偏增量的表达式,求z=f(x,y)给出变换,将已知偏微分方程化为常微分方程,求f(u)给出变换,将已知偏微分方程化为指定偏微分方程,求参数