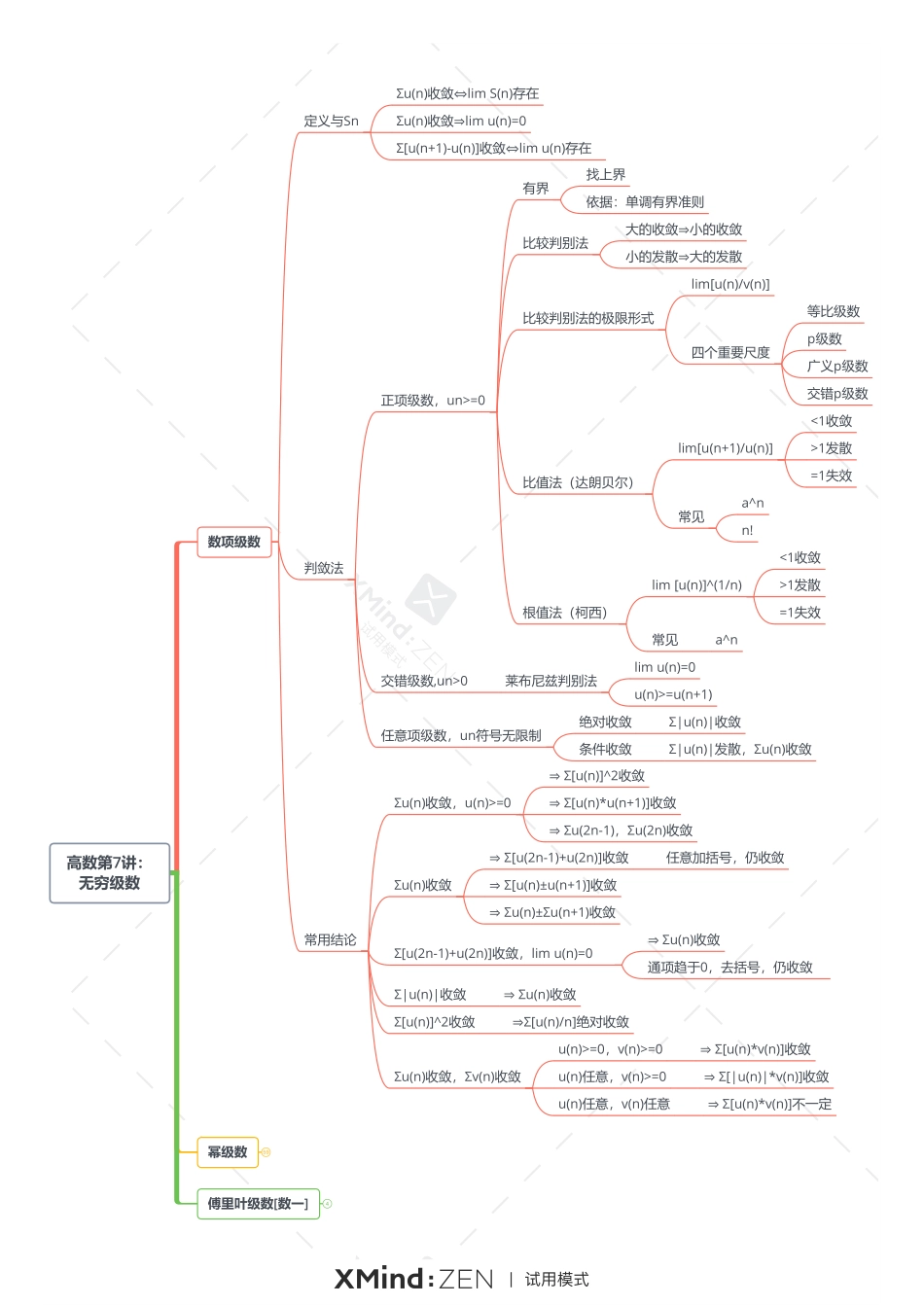
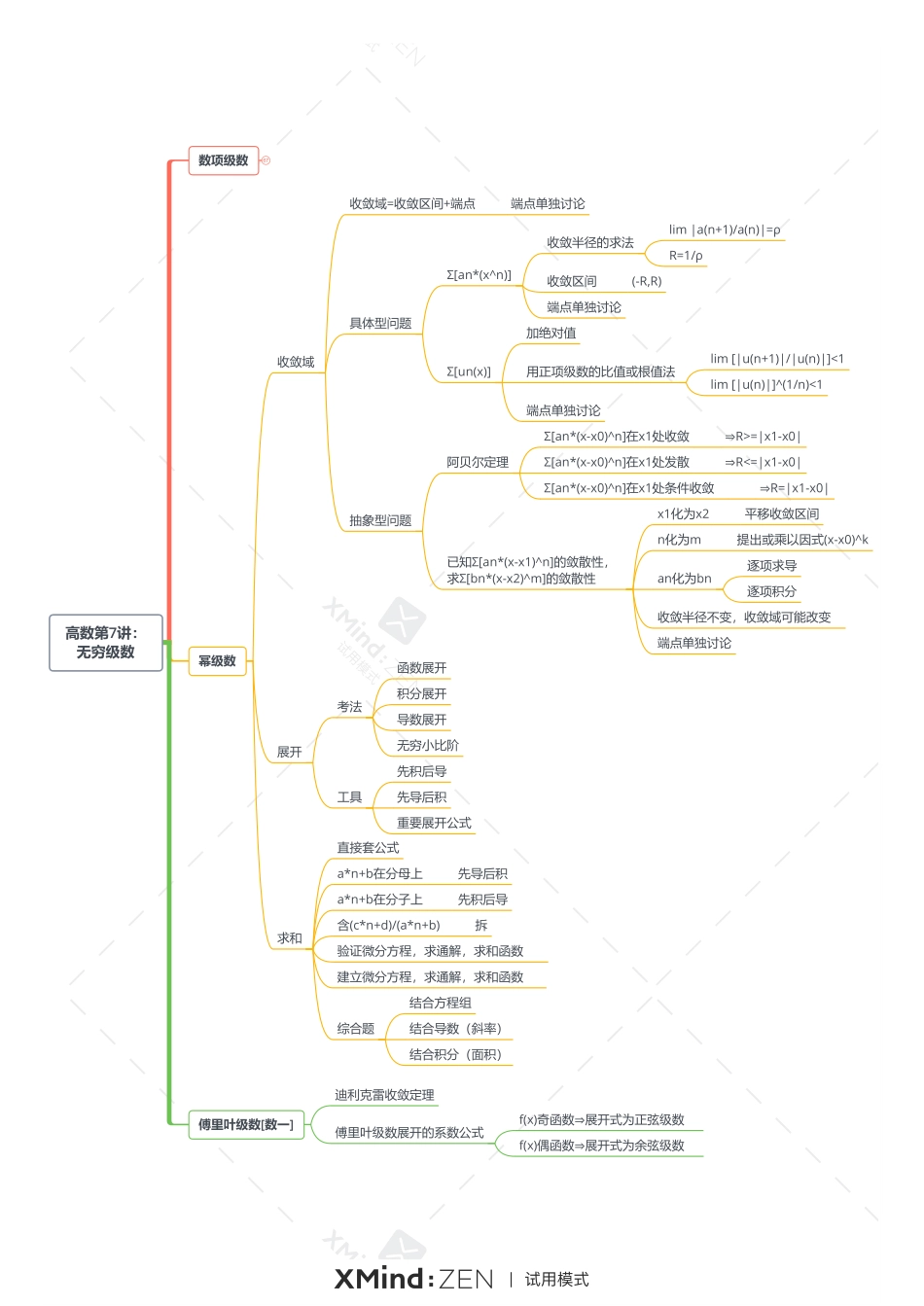
高数第7讲:无穷级数数项级数定义与SnΣu(n)收敛⇔limS(n)存在Σu(n)收敛⇒limu(n)=0Σ[u(n+1)-u(n)]收敛⇔limu(n)存在判敛法正项级数,un>=0有界找上界依据:单调有界准则比较判别法大的收敛⇒小的收敛小的发散⇒大的发散比较判别法的极限形式lim[u(n)/v(n)]四个重要尺度等比级数p级数广义p级数交错p级数比值法(达朗贝尔)lim[u(n+1)/u(n)]<1收敛>1发散=1失效常见a^nn!根值法(柯西)lim[u(n)]^(1/n)<1收敛>1发散=1失效常见a^n交错级数,un>0莱布尼兹判别法limu(n)=0u(n)>=u(n+1)任意项级数,un符号无限制绝对收敛Σ|u(n)|收敛条件收敛Σ|u(n)|发散,Σu(n)收敛常用结论Σu(n)收敛,u(n)>=0⇒Σ[u(n)]^2收敛⇒Σ[u(n)*u(n+1)]收敛⇒Σu(2n-1),Σu(2n)收敛Σu(n)收敛⇒Σ[u(2n-1)+u(2n)]收敛任意加括号,仍收敛⇒Σ[u(n)±u(n+1)]收敛⇒Σu(n)±Σu(n+1)收敛Σ[u(2n-1)+u(2n)]收敛,limu(n)=0⇒Σu(n)收敛通项趋于0,去括号,仍收敛Σ|u(n)|收敛⇒Σu(n)收敛Σ[u(n)]^2收敛⇒Σ[u(n)/n]绝对收敛Σu(n)收敛,Σv(n)收敛u(n)>=0,v(n)>=0⇒Σ[u(n)*v(n)]收敛u(n)任意,v(n)>=0⇒Σ[|u(n)|*v(n)]收敛u(n)任意,v(n)任意⇒Σ[u(n)*v(n)]不一定幂级数59傅里叶级数[数一]4高数第7讲:无穷级数数项级数67幂级数收敛域收敛域=收敛区间+端点端点单独讨论具体型问题Σ[an*(x^n)]收敛半径的求法lim|a(n+1)/a(n)|=ρR=1/ρ收敛区间(-R,R)端点单独讨论Σ[un(x)]加绝对值用正项级数的比值或根值法lim[|u(n+1)|/|u(n)|]<1lim[|u(n)|]^(1/n)<1端点单独讨论抽象型问题阿贝尔定理Σ[an*(x-x0)^n]在x1处收敛⇒R>=|x1-x0|Σ[an*(x-x0)^n]在x1处发散⇒R<=|x1-x0|Σ[an*(x-x0)^n]在x1处条件收敛⇒R=|x1-x0|已知Σ[an*(x-x1)^n]的敛散性,求Σ[bn*(x-x2)^m]的敛散性x1化为x2平移收敛区间n化为m提出或乘以因式(x-x0)^kan化为bn逐项求导逐项积分收敛半径不变,收敛域可能改变端点单独讨论展开考法函数展开积分展开导数展开无穷小比阶工具先积后导先导后积重要展开公式求和直接套公式a*n+b在分母上先导后积a*n+b在分子上先积后导含(c*n+d)/(a*n+b)拆验证微分方程,求通解,求和函数建立微分方程,求通解,求和函数综合题结合方程组结合导数(斜率)结合积分(面积)傅里叶级数[数一]迪利克雷收敛定理傅里叶级数展开的系数公式f(x)奇函数⇒展开式为正弦级数f(x)偶函数⇒展开式为余弦级数