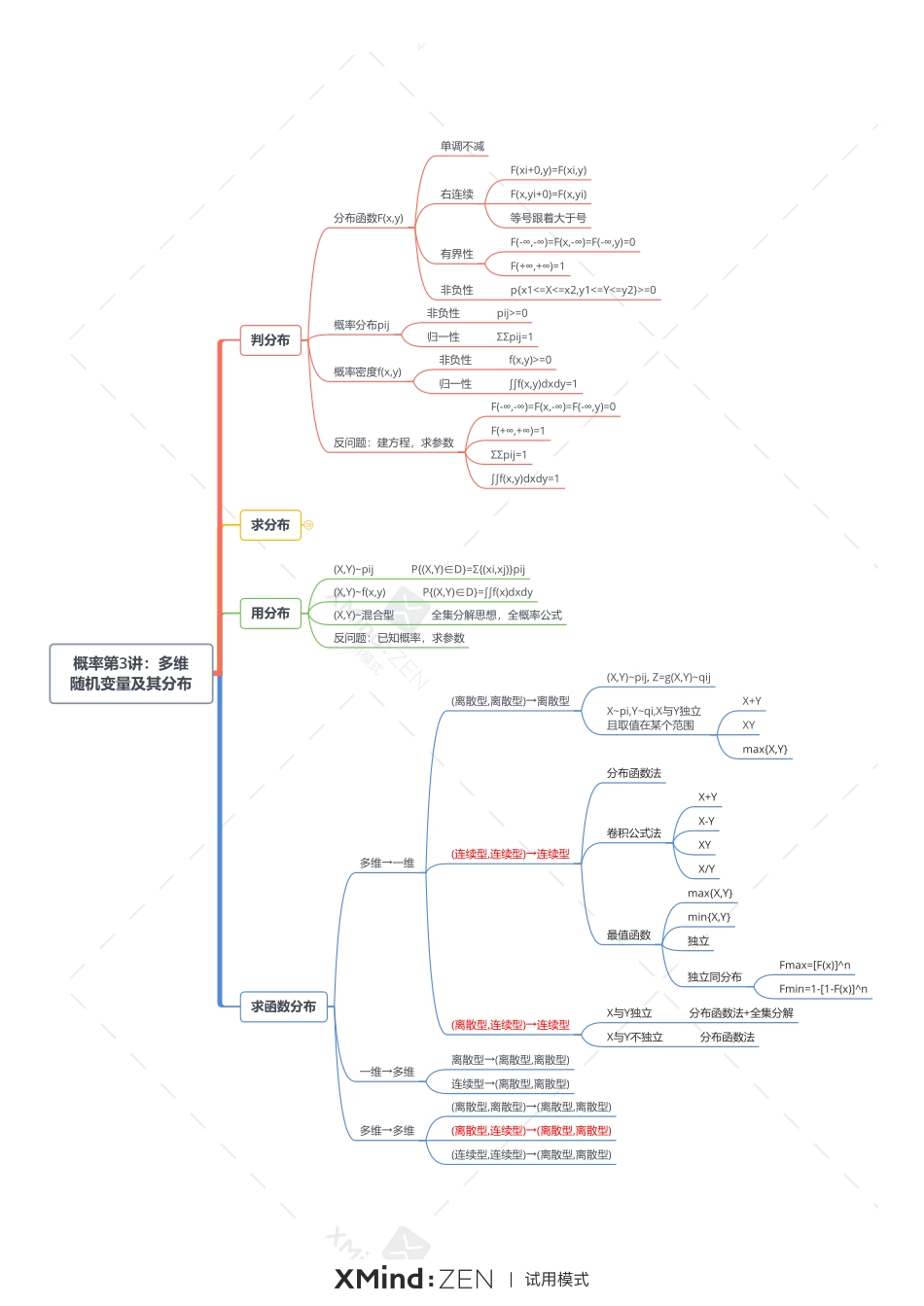
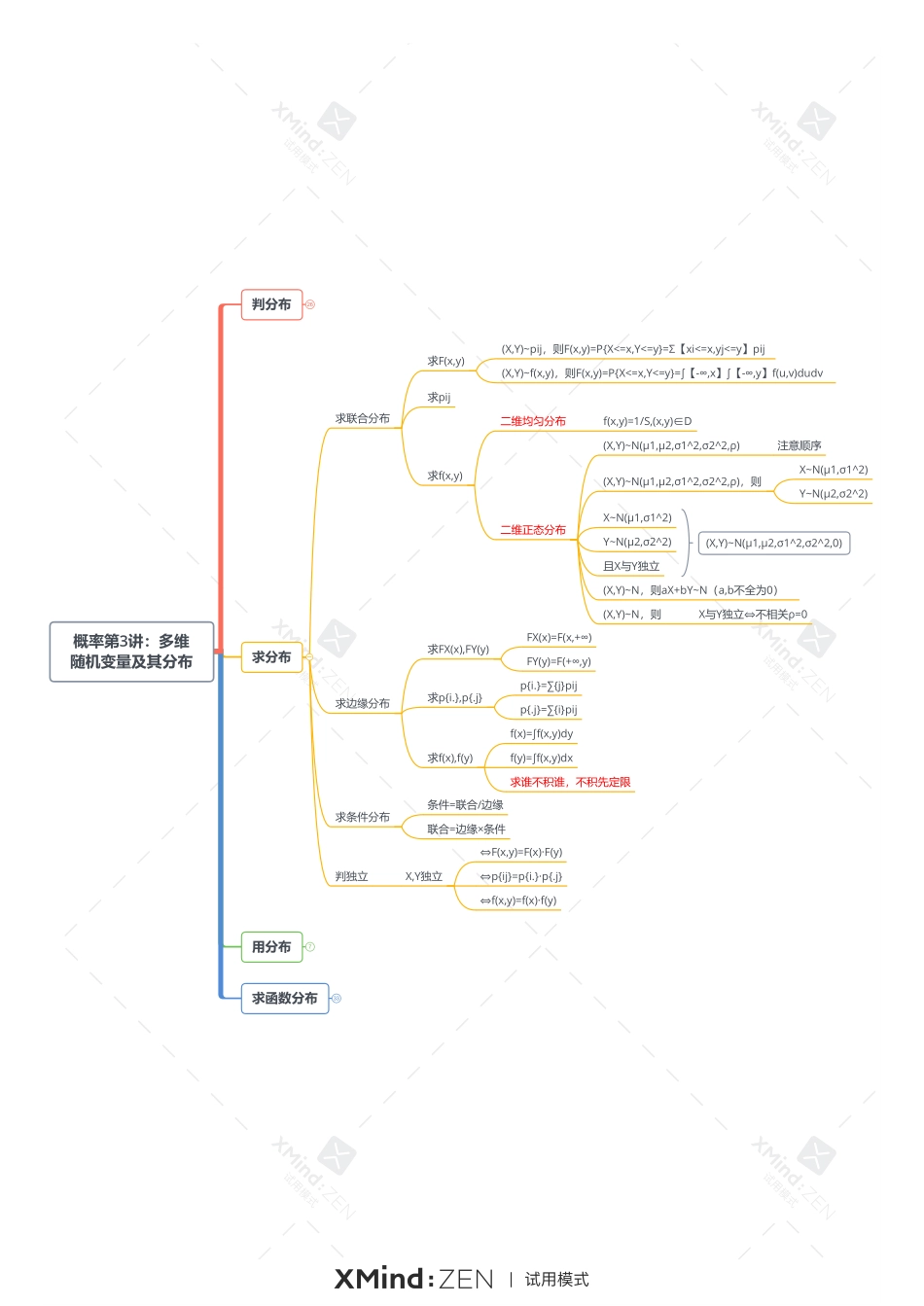
概率第3讲:多维随机变量及其分布求分布39用分布(X,Y)~pijP{(X,Y)∈D}=Σ{(xi,xj)}pij(X,Y)~f(x,y)P{(X,Y)∈D}=∫∫f(x)dxdy(X,Y)~混合型全集分解思想,全概率公式反问题:已知概率,求参数求函数分布一维→多维离散型→(离散型,离散型)连续型→(离散型,离散型)多维→多维(离散型,离散型)→(离散型,离散型)(离散型,连续型)→(离散型,离散型)(连续型,连续型)→(离散型,离散型)多维→一维(离散型,离散型)→离散型(离散型,连续型)→连续型X与Y独立分布函数法+全集分解X与Y不独立分布函数法(X,Y)~pij,Z=g(X,Y)~qijX~pi,Y~qi,X与Y独立且取值在某个范围X+YXYmax{X,Y}(连续型,连续型)→连续型分布函数法卷积公式法最值函数X+YXYmax{X,Y}X-YX/Ymin{X,Y}独立独立同分布Fmax=[F(x)]^nFmin=1-[1-F(x)]^n判分布分布函数F(x,y)单调不减右连续F(xi+0,y)=F(xi,y)F(x,yi+0)=F(x,yi)等号跟着大于号有界性F(-∞,-∞)=F(x,-∞)=F(-∞,y)=0F(+∞,+∞)=1非负性p{x1<=X<=x2,y1<=Y<=y2}>=0概率分布pij非负性pij>=0归一性ΣΣpij=1概率密度f(x,y)非负性f(x,y)>=0归一性∫∫f(x,y)dxdy=1反问题:建方程,求参数F(-∞,-∞)=F(x,-∞)=F(-∞,y)=0F(+∞,+∞)=1ΣΣpij=1∫∫f(x,y)dxdy=1概率第3讲:多维随机变量及其分布求分布求联合分布求F(x,y)(X,Y)~pij,则F(x,y)=P{X<=x,Y<=y}=Σ【xi<=x,yj<=y】pij(X,Y)~f(x,y),则F(x,y)=P{X<=x,Y<=y}=∫【-∞,x】∫【-∞,y】f(u,v)dudv求pij求f(x,y)二维均匀分布f(x,y)=1/S,(x,y)∈D二维正态分布(X,Y)~N(μ1,μ2,σ1^2,σ2^2,ρ)注意顺序(X,Y)~N(μ1,μ2,σ1^2,σ2^2,ρ),则X~N(μ1,σ1^2)Y~N(μ2,σ2^2)X~N(μ1,σ1^2)Y~N(μ2,σ2^2)且X与Y独立(X,Y)~N,则aX+bY~N(a,b不全为0)(X,Y)~N,则X与Y独立⇔不相关ρ=0(X,Y)~N(μ1,μ2,σ1^2,σ2^2,0)求边缘分布求FX(x),FY(y)FX(x)=F(x,+∞)FY(y)=F(+∞,y)求p{i.},p{.j}p{i.}=∑{j}pijp{.j}=∑{i}pij求f(x),f(y)f(x)=∫f(x,y)dyf(y)=∫f(x,y)dx求谁不积谁,不积先定限求条件分布条件=联合/边缘联合=边缘×条件判独立X,Y独立⇔F(x,y)=F(x)·F(y)⇔p{ij}=p{i.}·p{.j}⇔f(x,y)=f(x)·f(y)用分布7求函数分布33判分布26