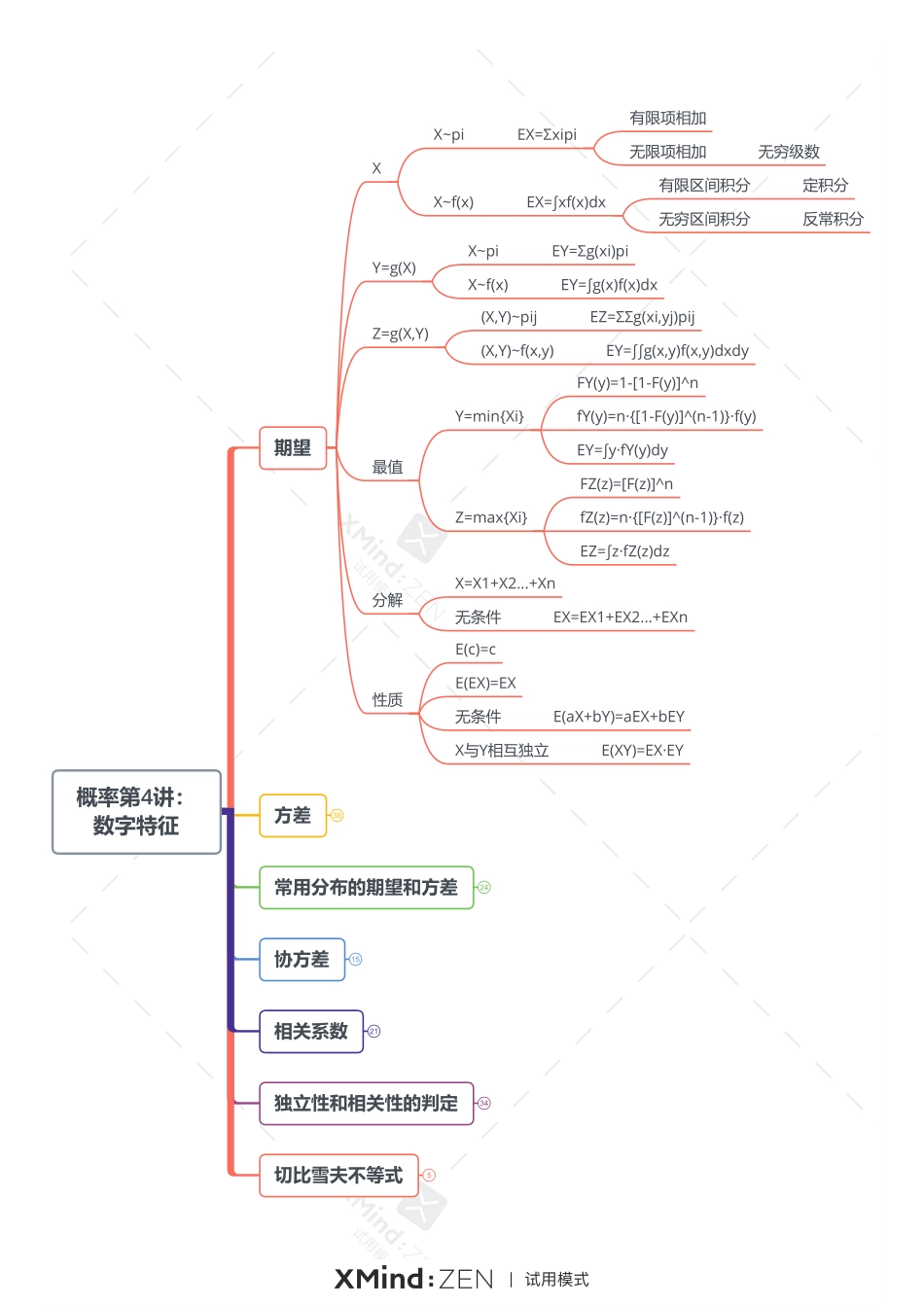
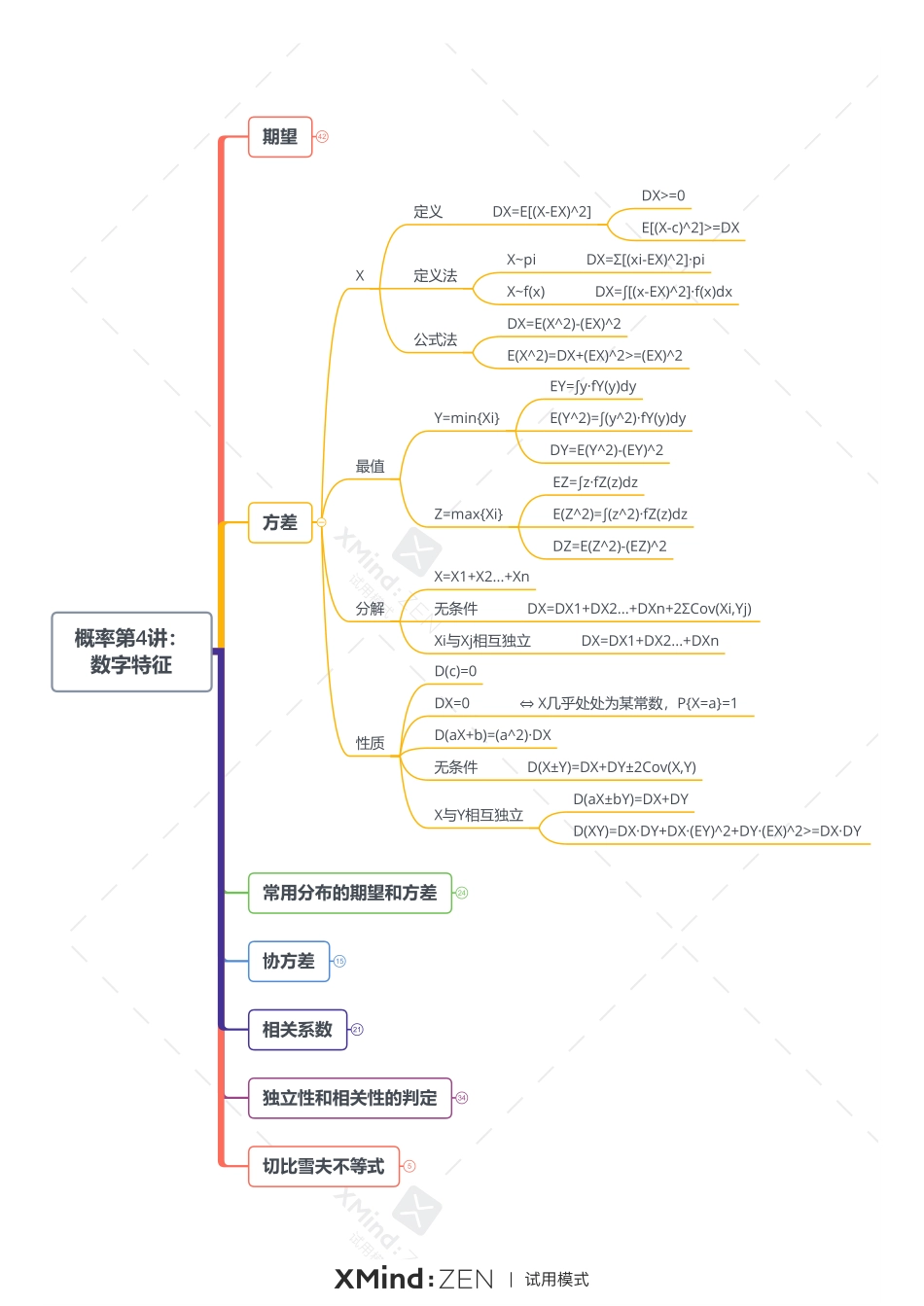
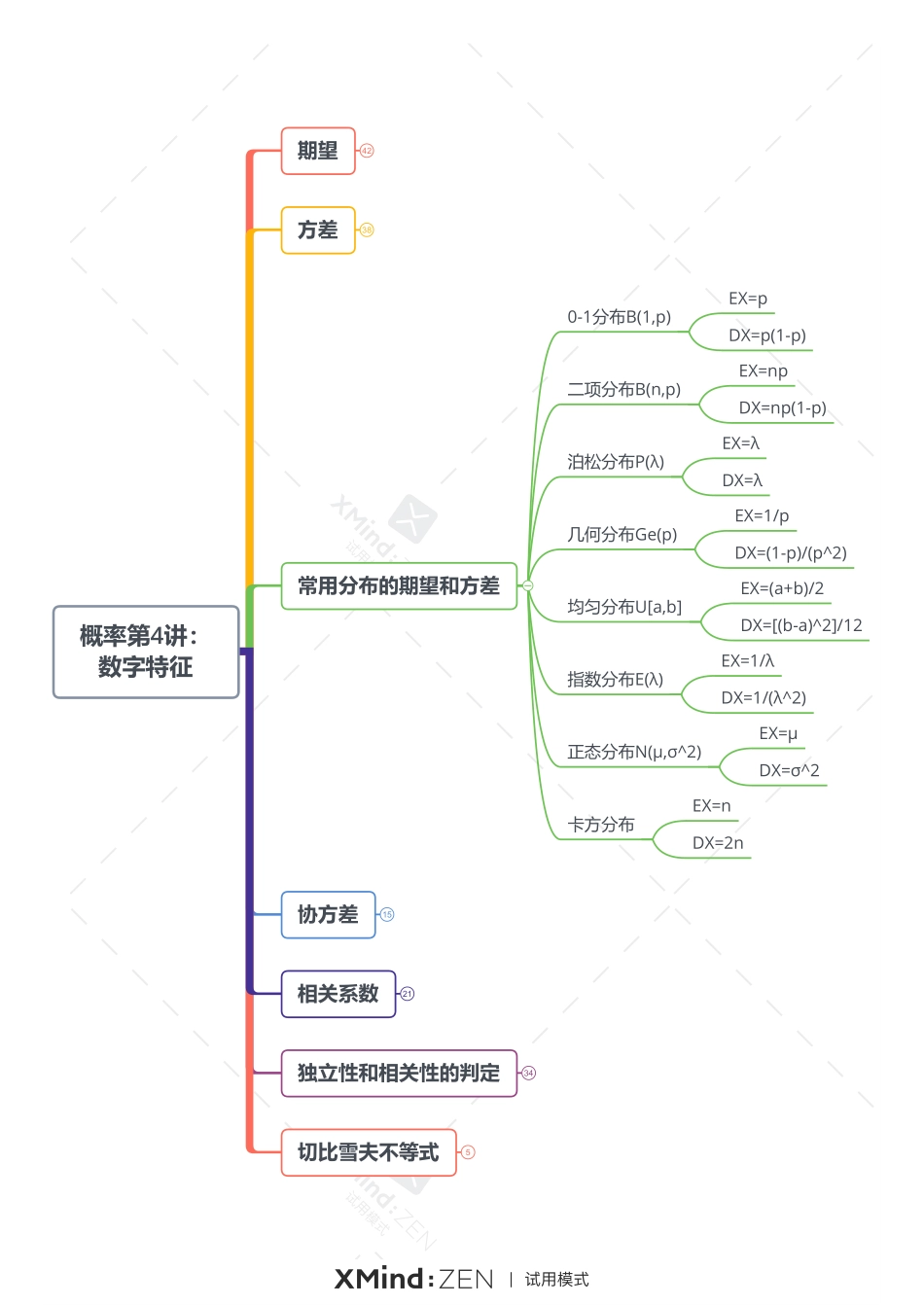
概率第4讲:数字特征期望XX~piEX=Σxipi有限项相加无限项相加无穷级数X~f(x)EX=∫xf(x)dx有限区间积分定积分无穷区间积分反常积分Y=g(X)X~piEY=Σg(xi)piX~f(x)EY=∫g(x)f(x)dxZ=g(X,Y)(X,Y)~pijEZ=ΣΣg(xi,yj)pij(X,Y)~f(x,y)EY=∫∫g(x,y)f(x,y)dxdy最值Y=min{Xi}FY(y)=1-[1-F(y)]^nfY(y)=n·{[1-F(y)]^(n-1)}·f(y)EY=∫y·fY(y)dyZ=max{Xi}FZ(z)=[F(z)]^nfZ(z)=n·{[F(z)]^(n-1)}·f(z)EZ=∫z·fZ(z)dz分解X=X1+X2...+Xn无条件EX=EX1+EX2...+EXn性质E(c)=cE(EX)=EX无条件E(aX+bY)=aEX+bEYX与Y相互独立E(XY)=EX·EY方差38常用分布的期望和方差24协方差15独立性和相关性的判定34切比雪夫不等式5相关系数21概率第4讲:数字特征期望42方差X定义DX=E[(X-EX)^2]DX>=0E[(X-c)^2]>=DX定义法X~piDX=Σ[(xi-EX)^2]·piX~f(x)DX=∫[(x-EX)^2]·f(x)dx公式法DX=E(X^2)-(EX)^2E(X^2)=DX+(EX)^2>=(EX)^2最值Y=min{Xi}EY=∫y·fY(y)dyE(Y^2)=∫(y^2)·fY(y)dyDY=E(Y^2)-(EY)^2Z=max{Xi}EZ=∫z·fZ(z)dzE(Z^2)=∫(z^2)·fZ(z)dzDZ=E(Z^2)-(EZ)^2分解X=X1+X2...+Xn无条件DX=DX1+DX2...+DXn+2ΣCov(Xi,Yj)Xi与Xj相互独立DX=DX1+DX2...+DXn性质D(c)=0DX=0⇔X几乎处处为某常数,P{X=a}=1D(aX+b)=(a^2)·DX无条件D(X±Y)=DX+DY±2Cov(X,Y)X与Y相互独立D(aX±bY)=DX+DYD(XY)=DX·DY+DX·(EY)^2+DY·(EX)^2>=DX·DY常用分布的期望和方差24协方差15独立性和相关性的判定34切比雪夫不等式5相关系数21概率第4讲:数字特征期望42方差38常用分布的期望和方差0-1分布B(1,p)EX=pDX=p(1-p)二项分布B(n,p)EX=npDX=np(1-p)泊松分布P(λ)EX=λDX=λ几何分布Ge(p)EX=1/pDX=(1-p)/(p^2)均匀分布U[a,b]EX=(a+b)/2DX=[(b-a)^2]/12指数分布E(λ)EX=1/λDX=1/(λ^2)正态分布N(μ,σ^2)EX=μDX=σ^2卡方分布EX=nDX=2n协方差15独立性和相关性的判定34切比雪夫不等式5相关系数21概率第4讲:数字特征期望42方差38常用分布的期望和方差24协方差独立性和相关性的判定34切比雪夫不等式5相关系数定义Cov(X,Y)=E[(X-EX)(Y-EY)]Cov(X,X)=DX定义法(X,Y)~pijCov(X,Y)=ΣΣ[(xi-EX)(yj-EY)]·pij(X,Y)~f(x,y)EY=∫∫[(x-EX)(y-EY)]·f(x,y)dxdy公式法Cov(X,Y)=E(XY)-EX·EY性质Cov(X,Y)=Cov(Y,X)Cov(aX,bY)=ab·Cov(X,Y)Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)单个可拆定义ρ{XY}=Cov(X,Y)/[(√DX)·(√DY)]线性相依性量纲为1,无单位ρ=0⇔X与Y不相关ρ≠0⇔X与Y相关性质-1<=ρ{XY}<=1ρ{XY}=1⇔P{Y=aX+b...