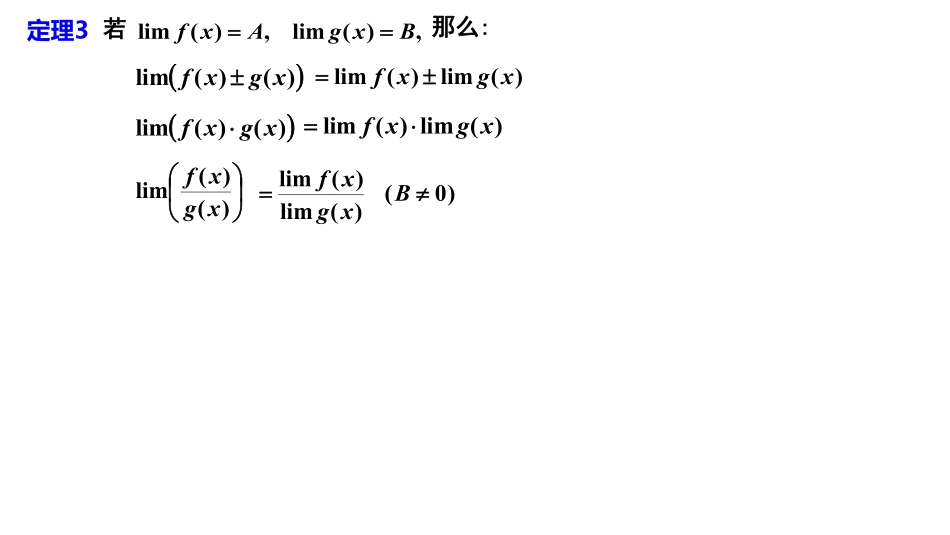07.1.8笔记小结【公众号：小盆学长】免费分享.pdfVIP免费

第一章函数与极限第五节极限运算法则有限个无穷小的积仍是无穷小.两个无穷小的和是无穷小.有界函数与无穷小的乘积是无穷小.定理1定理2常数与无穷小的乘积是无穷小.推论1推论2定理3,)(lim,)(limBxgAxf那么:若)()(limxgxf)()(limxgxf)()(limxgxf)(lim)(limxgxf)(lim)(limxgxf)(lim)(limxgxf)0(B如果推论1存在,而为常数,那么)(limxfc)(lim)(limxfcxcf如果推论1存在,而是正整数,那么)(limxfnnnxfxf)]([lim)(lim,lim,limbbaannnn定理4设则;limlim)(lim)1(bababannnnnnn;limlim)(lim)2(abbabannnnnnn)0.limlimlim)3(bbababannnnnnn（【例1】)2(lim22xxx【例2】53lim321xxxxx【例3】23lim321xxxxx【例4】23lim32xxxxx01110111limbxbxbxbaxaxaxammmmnnnnx.,,,0,,mnmnmnbamn定理5如果),()(xx而那么,)(lim,)(limBxAx.BA是由)(xgu复合而成，0)(lim0uxgxx且),(00xUx当时，则.)]([lim0axgfxx设)]([xgfy),(ufy,)(lim0aufuu,)(0uxg定理6内容小结1.极限运算法则(1)无穷小运算法则(2)极限四则运算法则(3)复合函数极限运算法则注意使用条件2.求函数极限的方法(1)分式函数极限求法0)1xx时,用代入法(要求分母不为0)0)2xx时,对00型,约去分母零因子x)3时,分子分母同除最高次幂“抓大头”(2)复合函数极限求法设中间变量作业P45：1（12）（13）（14）；3;4；5.