01.考研数学预备知识0基础知识点09讲义【公众号：小盆学长】免费分享.pdfVIP免费

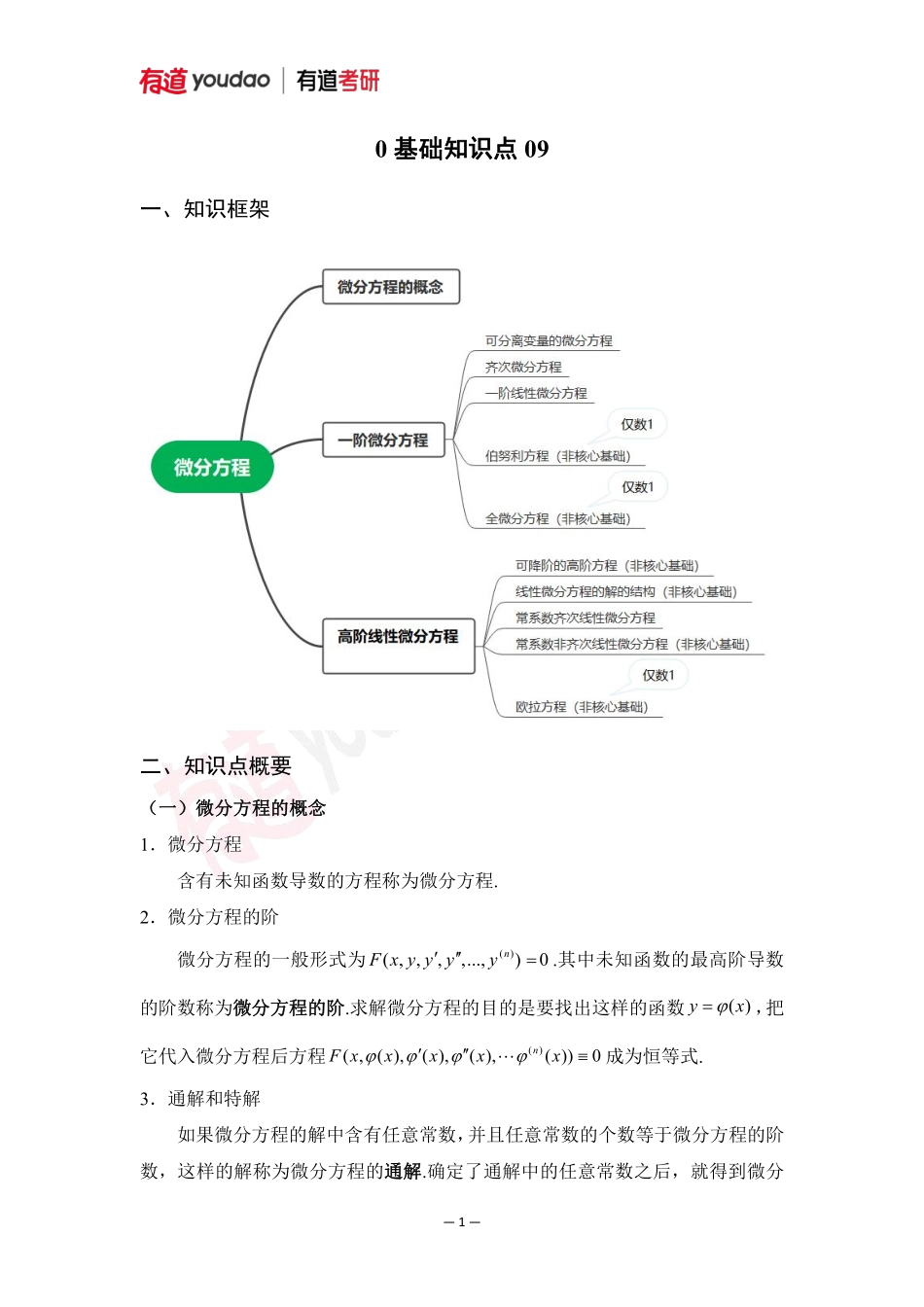
—1—0基础知识点09一、知识框架二、知识点概要（一）微分方程的概念1．微分方程含有未知函数导数的方程称为微分方程.2．微分方程的阶微分方程的一般形式为()(,,,,...,)0nFxyyyy.其中未知函数的最高阶导数的阶数称为微分方程的阶.求解微分方程的目的是要找出这样的函数()yx，把它代入微分方程后方程()(,(),(),(),())0nFxxxxx成为恒等式.3．通解和特解如果微分方程的解中含有任意常数，并且任意常数的个数等于微分方程的阶数，这样的解称为微分方程的通解.确定了通解中的任意常数之后，就得到微分—2—方程的特解.如果微分方程是一阶的，则确定通解中任意常数的初始条件一般是00()yxy；如果微分方程是二阶的，则确定通解中任意常数的初始条件一般是0000(),()yxyyxy.（二）一阶微分方程1.可分离变量方程形如：()()yfxgy解法：分离变量得()()dyfxdxgy，所以()()dyfxdxgy.2.齐次方程形如：yyfx解法：令yux，则yux，'duyuxdx，原方程()duuxfudxln||()()dudxduxCfuuxfuu.3.一阶线性微分方程形如：()()yPxyQx解法：（1）方程两边同乘积分因子()Pxdxe，然后积分化简：()()()PxdxPxdxyeQxedxC.（2）直接代入通解公式：()()()PxdxPxdxyeQxedxC（三）高阶线性微分方程1.二阶常系数齐次线性微分方程形如：'''0ypyqy其中,pq均为常数—3—解法：特征方程为20pq（1）当12,为不同的特征根时，齐次方程的通解为1212()xxyxCeCe.（2）当12时，齐次方程的通解为12()()xyxCCxe.（3）当i（复根）时，齐次方程的通解为12()(cossin)xyxeCxCx三、练习题例1.求微分方程2y40dxxxdy的通解例2.求微分方程2223220xxyydxxxydy的通解.例3.微分方程tancosyyxx的通解为y_________.例4.求下列微分方程的通解.（1）320yyy（2）20yyy（3）220yyy