01.考研数学预备知识0基础知识点04讲义【公众号：小盆学长】免费分享.pdfVIP免费

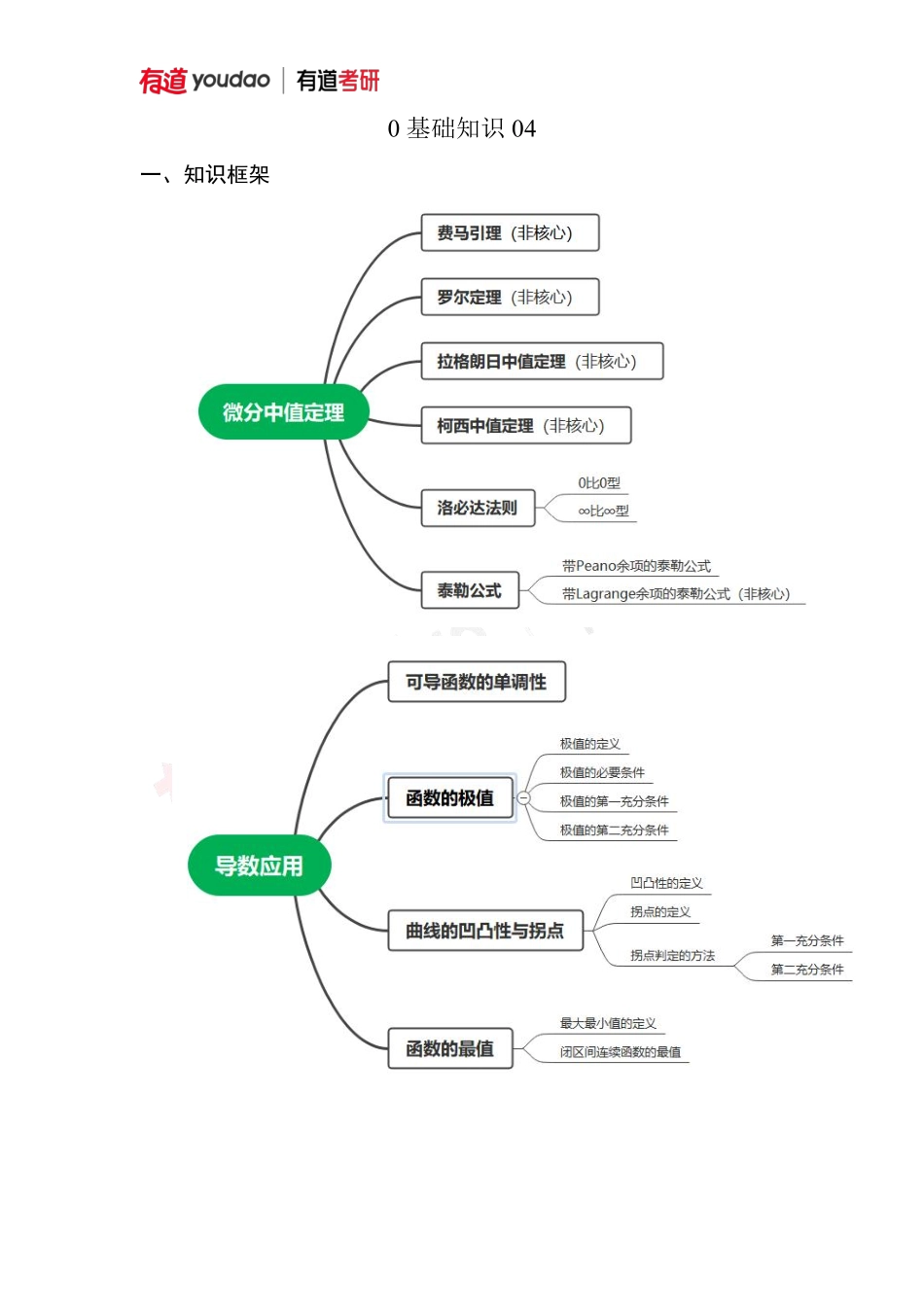
0基础知识04一、知识框架二、知识点概要1.定理1（洛必达法则）设(),()fxgx满足：（1）0)(lim)(limxgxf或)(lim)(limxgxf；（2）(),()fxgx在极限点的附近均可导且0)(xg（3）)()(limxgxf为某常数A或为.则有)()(lim)()(limxgxfxgxf.2.定理2（泰勒公式）（1）（泰勒中值定理）设)(xf在0xx的邻域内有直到1n阶导数，则有200000000[]2!!nnnfxfxfxfxfxxxxxxxoxxn称此种形式的余项为佩亚诺型余项.特别地，若00x，则20000()2!!nnnfffxffxxxoxn称为麦克劳林公式.（2）常用函数在0x处的泰勒公式：211e1()2!!xnnxxxoxn23111ln(1)(1)()23nnnxxxxxoxn2131211sin(1)()3!(21)!nnnxxxxoxn2221cos1(1)()2!(2)!nnnxxxoxn331arcsin()6xxxox331tan()3xxxox331arctan()3xxxox211()1nnxxxoxx211(1)()1nnnxxxoxx2(1)(1)12!mmmxmxx(1)(1)()!nnmmmnxoxn3.函数单调性的判定设函数()yfx在[,]ab上连续，在(,)ab内可导，1）若在(,)ab内0)(xf,则函数()yfx在[,]ab上单调增加；2）若在(,)ab内0)(xf,则函数()yfx在[,]ab上单调减少．4.极值（1）定义若存在0x的某邻域0xU，使得对任意的0xUx，都有0()()fxfx，则称0x为()fx的极大值点，0()fx为()fx的极大值.类似的可定义极小值.（2）极值的必要条件)(xf在0x处可导，且)(xf在0x取得极值，则0)(0xf（3）极值的充分条件定理1（第一充分条件）设函数()fx在0x处连续，并在0x的某去心邻域0(,)Ux内可导：1）若00(,)xxx时，()0fx，而00(,)xxx时，()0fx，则()fx在0x处取得极大值；2）若00(,)xxx时，()0fx，而00(,)xxx时，()0fx，则()fx在0x处取得极小值；3）若0,xUx时，()fx符号保持不变，则()fx在0x处没有极值.定理2（第二充分条件）设)(xf在0xx处具有二阶导数，且0)(0xf，则1）若0)(0xf，则0xx为)(xf的极小点；2）若0()0fx，则0xx为)(xf的极大点；3）若0)(0xf，则0xx可能是)(xf的极值点，也可能不是.5.函数的凹凸性与拐点（1）凹凸性1）定义：设函数()fx在区间I上连续，任取两点12,xxI，恒有1212()()()2...