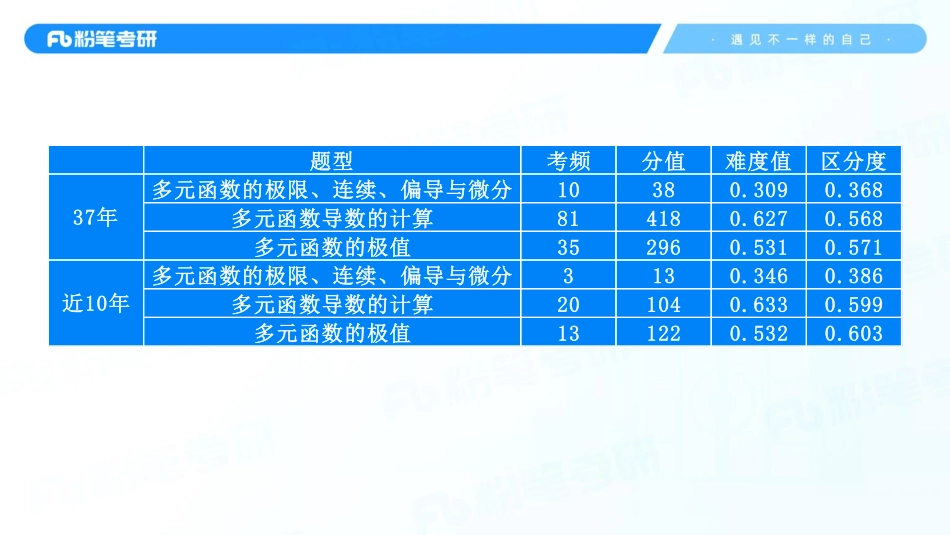
第十章——多元函数微分学1(讲义+笔记)主讲教师:考研数学李振授课时间:2024.03.06粉笔考研·官方微信题型考频分值难度值区分度多元函数的极限、连续、偏导与微分10380.3090.368多元函数导数的计算814180.6270.568多元函数的极值352960.5310.571多元函数的极限、连续、偏导与微分3130.3460.386多元函数导数的计算201040.6330.599多元函数的极值131220.5320.60337年近10年1第十章——多元函数微分学1(笔记)【注意】多元函数微分学考情:1.概念部分(多元函数的极限、连续、偏导与微分):考查都是小题,一旦出现,难度会比较高。2.计算(多元函数导数的计算):平均5、6分一个,有时候是小题,有时候是大题,主要以小题为主。3.应用(多元函数的极值):平均一个9分左右,主要是大题的形式出现,每年必考的一类题型。2【注意】多元函数的概念:“元”就是指自变量的个数,一元就只有一个自变量,一元中x∈D,D是一个区间。二元函数就有两个自变量,(x,y)∈D会形成一个区域。3【注意】1.多元函数的极限、连续、可导与可微:主要针对二元函数。2.二重极限:(1)当x在x0附近取值时,f(x)与A无限接近。①去心。②充要条件:可左可右。(2)当(x,y)在(x0,y0)附近取值时,f(x,y)与A无限接近。3.与一元函数极限计算的不同点:(1)去心。(2)极限存在的充要条件。【解析】1(1).分子可以直接用等价无穷小替换,具体步骤见上图。4【解析】1(2).出现了sin∞,无穷小量*有界量=无穷小量,则结果=0,具体步骤见上图。【解析】1(3).取特殊路径说明极限存在。路径一:y=x,原式=lim𝑥→0𝑥²2𝑥²=12。路径二:y=-x,原式=lim𝑥→0−𝑥²2𝑥²=−12。两个极限不相等,说明原极限不存在。也可以取一般路径,具体步骤见上图。5【解析】1(4).考虑取一般路径,y=kx,原式=lim𝑥→0𝑘𝑥³𝑥2+𝑘²𝑥²=lim𝑥→0𝑘𝑥1+𝑘²=0。极限存在的充要条件是沿着任意路径趋近于(x0,y0)时,极限都存在。取特殊路径取不完,一类路径不能代表所有路径,所以取特殊路径只能说明极限不存在。将原式写成无穷小量*有界量=0,具体步骤见上图。6【解析】1(5).分子是三次,分母是2次和4次,分母不是齐次,就先凑成齐次,变量代换,令u=y²,原式=lim𝑥→0𝑢→0𝑥𝑢𝑥2+𝑢²,和第(3)题一样,所以极限不存在,具体步骤见上图。【注意】这也是一种取特殊路径。7【解析】1(6).分子是2次,分母是1次,分子次数大于分母次数,可以写成相乘的形式,但不是无穷小...