5.3实对称矩阵的相似对角化【公众号：小盆学长】免费分享.pdfVIP免费

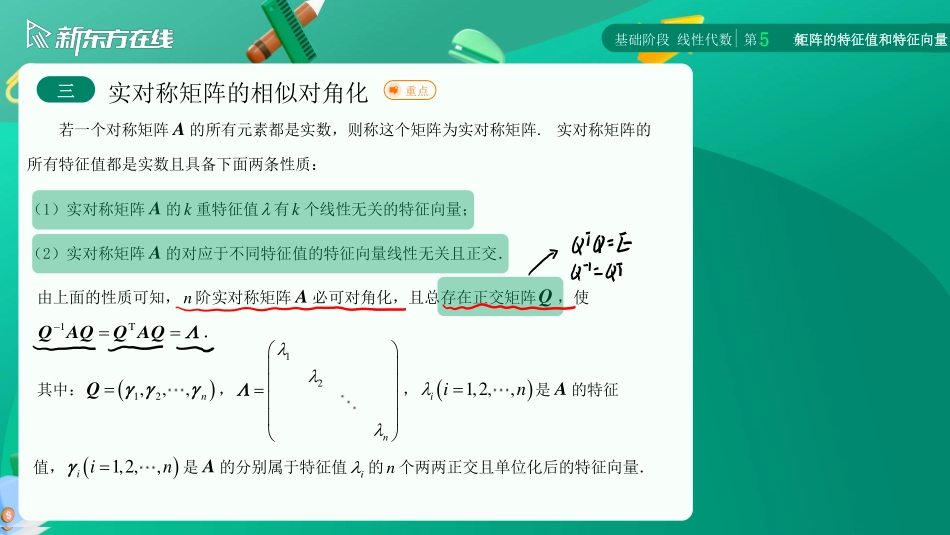
第五章矩阵的特征值和特征向量考研数学线性代数@新东方在线孟小玉基础阶段线性代数第章矩阵的特征值和特征向量5第五章矩阵的特征值和特征向量矩阵的特征值和特征向量一相似矩阵与矩阵的相似对角化二实对称矩阵的相似对角化三考研数学线性代数基础阶段线性代数第章矩阵的特征值和特征向量5三实对称矩阵的相似对角化重点若一个对称矩阵A的所有元素都是实数，则称这个矩阵为实对称矩阵.实对称矩阵的所有特征值都是实数且具备下面两条性质：（1）实对称矩阵A的k重特征值有k个线性无关的特征向量；（2）实对称矩阵A的对应于不同特征值的特征向量线性无关且正交．由上面的性质可知，n阶实对称矩阵A必可对角化，且总存在正交矩阵Q，使1TQAQQAQ．其中：12,,,nQ，12n，1,2,,iin是A的特征值，1,2,,iin是A的分别属于特征值i的n个两两正交且单位化后的特征向量．基础阶段线性代数第章矩阵的特征值和特征向量5【例5.13】已知矩阵222254245A.（1）求可逆矩阵P使1PAP;（2）求正交矩阵Q使TQAQ.222254245AE32222254011rr23242294001cc24(1)292(1)(10)0，基础阶段线性代数第章矩阵的特征值和特征向量5【例5.13】已知矩阵222254245A.（1）求可逆矩阵P使1PAP;（2）求正交矩阵Q使TQAQ.特征值为121，310.对121，解方程0AEx，122122244000244000AE，对310，解方程100AEx，110822210254011245000AE，则可逆矩阵1222101011P，使得11110PAP.基础阶段线性代数第章矩阵的特征值和特征向量5【例5.13】已知矩阵222254245A.（1）求可逆矩阵P使1PAP;（2）求正交矩阵Q使TQAQ.特征值为121，310.特征向量12221,00131211，已知3分别与12,正交，将12,正交化：令11210，2122111222(,)41014(...