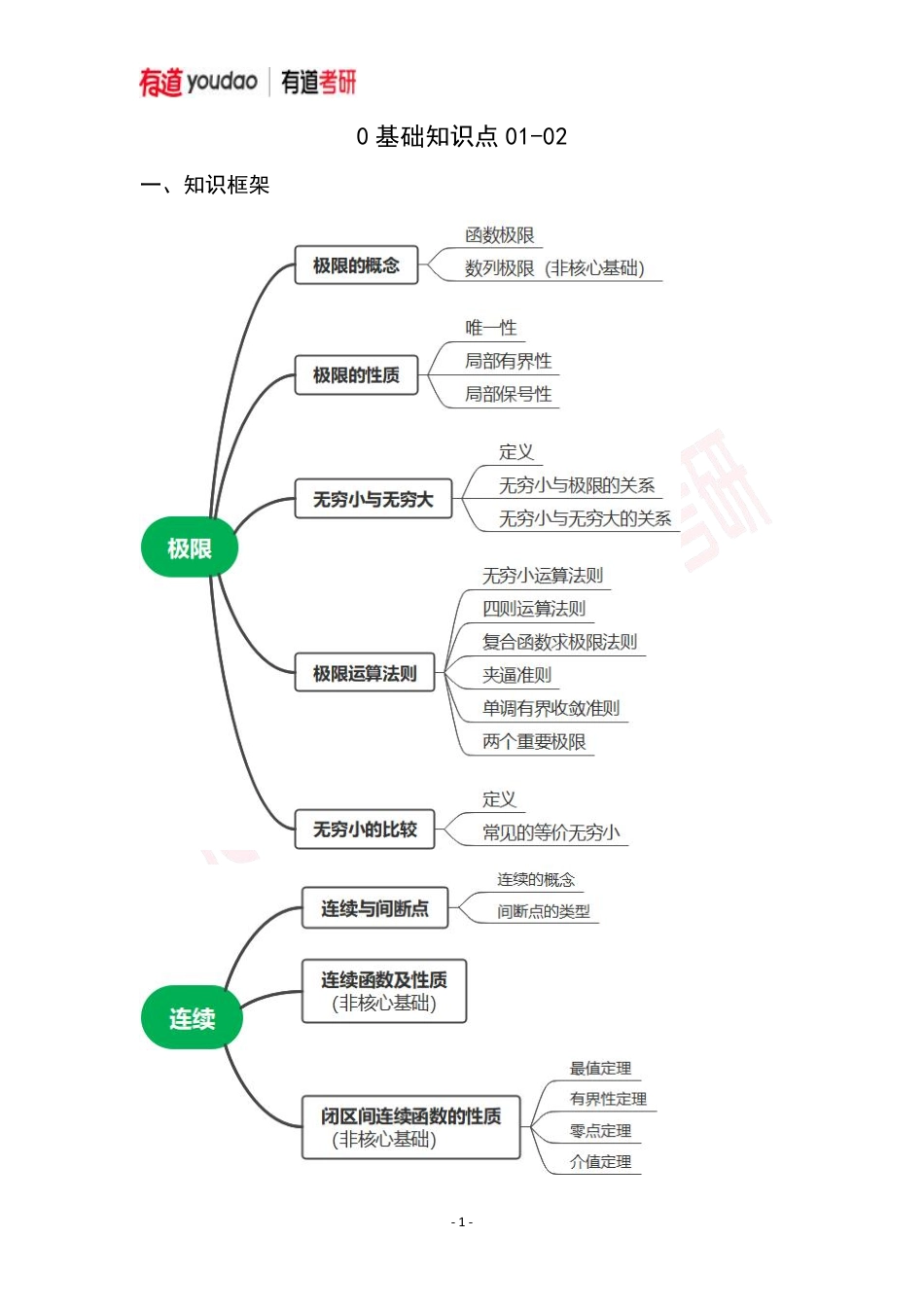
-1-0基础知识点01-02一、知识框架-2-二、知识点概要1.极限的概念00lim()()(),lim()0xxxxfxAfxAxx其中.2.极限的性质(1)局部有界性:设0lim()xxfxA,则存在0,当00(,)xxx且0xx时,()fx有界.(2)局部保号性:设0lim()xxfxA,若0(0)AA或,则存在0,当00(,)xxx且0xx时,()0fx(或()0fx).3.无穷小与无穷大(1)定义如果函数()fx当0xx或(x)时的极限为零,则称()fx为0xx或(x)时的无穷小量。若0lim()xxfx,则称()fx为0xx时的无穷大量。(2)无穷小与无穷大的关系在同一极限过程中,如果()fx为无穷大量,则1()fx为无穷小量;反之,如果()fx为无穷小量,且()0fx,则1()fx为无穷大量。4.极限运算法则(1)无穷小运算法则两个无穷小的和是无穷小;有界函数与无穷小的乘积是无穷小。(2)四则运算法则若lim(),lim()fxAgxB,则:lim(()())lim()lim()fxgxfxgxAB;lim()()lim()lim()fxgxfxgxAB;-3-.()lim()lim(0)()lim()fxfxABgxgxB(3)复合函数求极限法则设()yfgx是由(),()yfxugx复合而成,00lim()xxgxu且0lim()uufua,当00(,)xUx时,0()gxu,则0lim()xxfgxa(4)夹逼准则设在0xx的某去心邻域内,恒有)()()xfxx(,且00lim()lim()xxxxxxA,则0lim()xxfxA.(5)单调有界收敛准则单调有界数列必有极限.若数列单调增加(单调减少)有上界(下界),则数列必有极限.(6)两个重要极限0sinlim1xxx,10lim(1)xxxe.5.无穷小的比较(1)lim)0,lim()0,()0xxx设(,则:()lim0,())()xxxx若则称是(的高阶无穷小,()(())xox记为.()lim,())()xxxx若则是(的低阶无穷小.()lim(0),())()xccxxx若则称与(是同阶无穷小,特别地,()lim1()xx若,则称()x与()x是等价无穷小,记为()()xx.()lim(0),0,())()kxcckxxkx若则是(的阶无穷小.(2)常见的等价无穷小当0x时,sinarcsintanarctanln(1)1xxxxxxe-4-211cos2xx,11(1)1nxxn.6.连续与间断点(1)连续概念若00lim()xxfxfx,则fx在0xx处连续.(2)间断点及其类型1)若00lim()xxfxfx存在,则fx在0xx处为可去间断点.2)若00limlimxxxxfxfx,存在但不相等,则fx在0xx处...