02.笔记小节【公众号：小盆学长】免费分享(2).pdfVIP免费

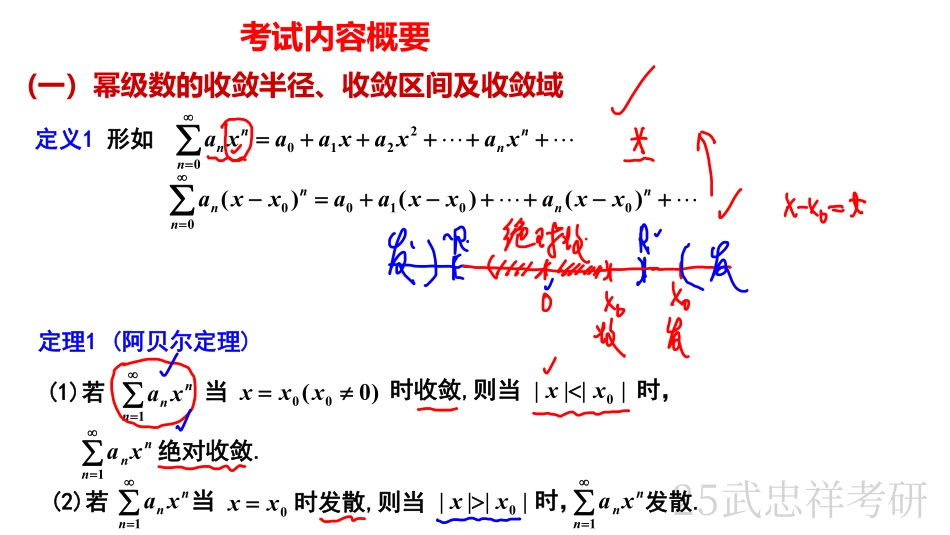
高数基础班（21）主讲武忠祥教授21幂级数（概念、性质、函数展开为幂级数，级数求和及举例）P164-P172本节内容要点一.考试内容概要(一）收敛半径收敛区间收敛域（二）幂级数的性质第二节幂级数二.常考题型与典型例题题型一求收敛半径、收敛区间及收敛域题型二将函数展开为幂级数题型三级数求和（三）函数的幂级数展开25武忠祥考研考试内容概要(一）幂级数的收敛半径、收敛区间及收敛域nnnnnxaxaxaaxa22100nnnnnxxaxxaaxxa)()()(001000定义1形如定理1(阿贝尔定理)1nnnxa)0(00xxx||||0xx1nnnxa当时收敛,则当时，绝对收敛.(1)若1nnnxa0xx||||0xx1nnnxa(2)若当时发散,则当时，发散.25武忠祥考研定理2幂级数0nnnxa的收敛性有且仅有以下三种可能（1）对任何),(x都收敛;（2）仅在0x处收敛;,RRxRx（3）存在一个正数当时绝对收敛,当时发散.0nnnxa0xx0x),(RR【注】若幂级数在点处条件收敛，则点必为该幂级数收敛区间的一个端点.25武忠祥考研,lim1nnnaa.1R定理3如果则,||limnnna.1R定理4如果则（二）幂级数的性质0nnnxa,1R0nnnxb,2R21,minRRR1)有理运算性质的收敛半径为的收敛半径为令，则当设（1)加减法：nnnnnnnnnnxbaxbxa)(000),(RRx（2)乘法：000)()(nnnnnnnnnxcxbxa0110bababacnnnn25武忠祥考研（3）除法:,000nnnnnnnnnxcxbxa2)分析性质：0nnnxaR).(xS设幂级数的收敛半径为,和函数为)(xS(1)连续性:在收敛域上连续;则)(xS),(RR(2)可导性:在上可导,且可逐项求导,半径不变.即0100)()(nnnnnnnnnxnaxaxaxS25武忠祥考研)(xS(3)可积性:在收敛域上可积,且可逐项积分,半径不变.即.11ddd)(0100000nnnnxnnxnnnxxanxxaxxaxxS（三）函数的幂级数展开)(xf),(00RxRx0xx,)()(00nnnxxaxf定理1如果函数在区间上能展开为的幂级数则,其展开式是唯一的，nnnxxnxf)(!)(000)()(xf0xx在处的泰勒级数.25武忠祥考研)(xf0xxnnnxxnxf)(!)(000)(),(00RxRx定理2设在处任意阶可导,则在上收敛于)(xf.0)(limxRnn10)1()()!1()()(nnnxxnfxR)(xf0x)()(!)()(000)(xRxxkxfxfnknkk...