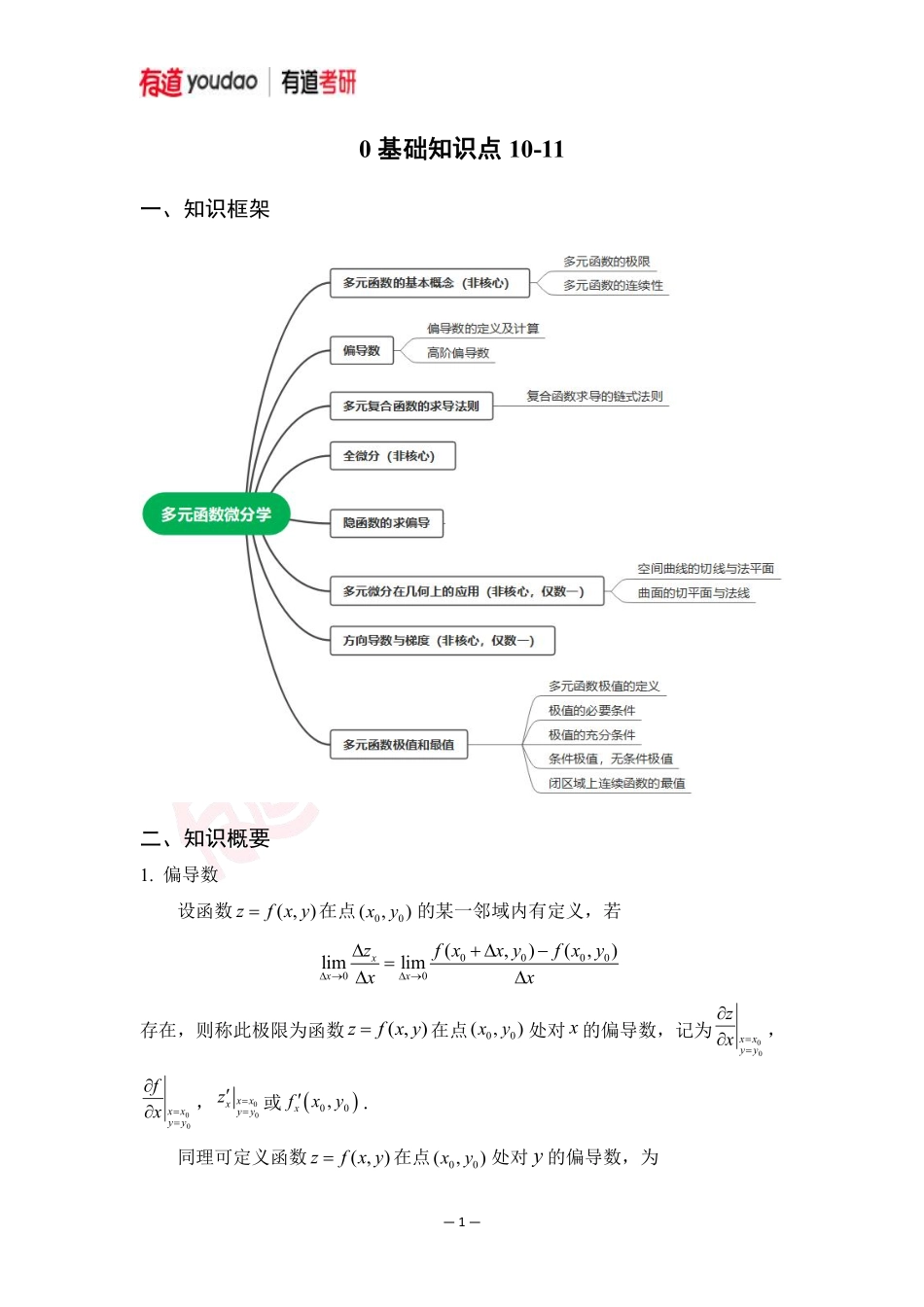
—1—0基础知识点10-11一、知识框架二、知识概要1.偏导数设函数),(yxfz在点),(00yx的某一邻域内有定义,若000000(,)(,)limlimxxxzfxxyfxyxx存在,则称此极限为函数),(yxfz在点),(00yx处对x的偏导数,记为00yyxxxz,00yyxxxf,00xxxyyz或00,xfxy.同理可定义函数),(yxfz在点),(00yx处对y的偏导数,为—2—000000(,)(,)limlimyyyzfxyyfxyyy,记为00yyxxyz,00yyxxyf,00xxyyyz或00,yfxy.同理可以定义,如果函数),(yxfz在区域D内任一点),(yx处对x的偏导数都存在,那么这个偏导数就是x、y的函数,称为函数),(yxfz对自变量x的偏导数,记作xz,xf,xz或,xfxy.),(yxfz对自变量y的偏导数,记作yz,yf,yz或(,)yfxy.2.高阶偏导数设有函数(,)zfxy,称)(22xzxxz,)(22yzyyz,2()zzxyyx,2()zzyxxy为函数的二阶偏导数,其中称),(),(2xzyyxzyxfxy),(),(2yzxxyzyxfyx为函数的二阶混合偏导数.3.复合函数求偏导(1)设,zfuv可偏导,,,uxyvxy可偏导,则yvvzyuuzyzxvvzxuuzxz.(2)设,zfuv可偏导,且uxvx可导,则dzfdufdvdxudxvdx.(3)设,,zfxuv可偏导,,,uxyvxy可偏导,则xvvfxuufxfxz,yvvfyuufyz.4.隐函数求偏导—3—设函数(,,)Fxyz在点000(,,)Pxyz的某邻域内具有连续的偏导数,且000000(,,)0,(,,)0zFxyzFxyz,则方程(,,)0Fxyz在点000(,,)xyz的某邻域内恒能惟一确定一个单值连续且具有连续偏导数的函数(,),zfxy它满足条件000(,)zfxy,并有,yxzzFFzzxFyF.5.二元函数的无条件极值(1)二元函数极值的定义设函数),(yxfz在点),(000yxp的某邻域内有定义,若对该邻域内异于0p的任意点),(yxp,总有00,,fxyfxy(或00,,fxyfxy)成立,则称),(00yxf是函数),(yxfz在点),(000yxp处取得的极小值(或极大值),并称点),(000yxp为),(yxfz的极小值点(或极大值点).极大值与极小值统称为...