高数第三章微分中值定理与导数应用25-35节课讲义-赵老师【公众号：小盆学长】免费分享.pdfVIP免费

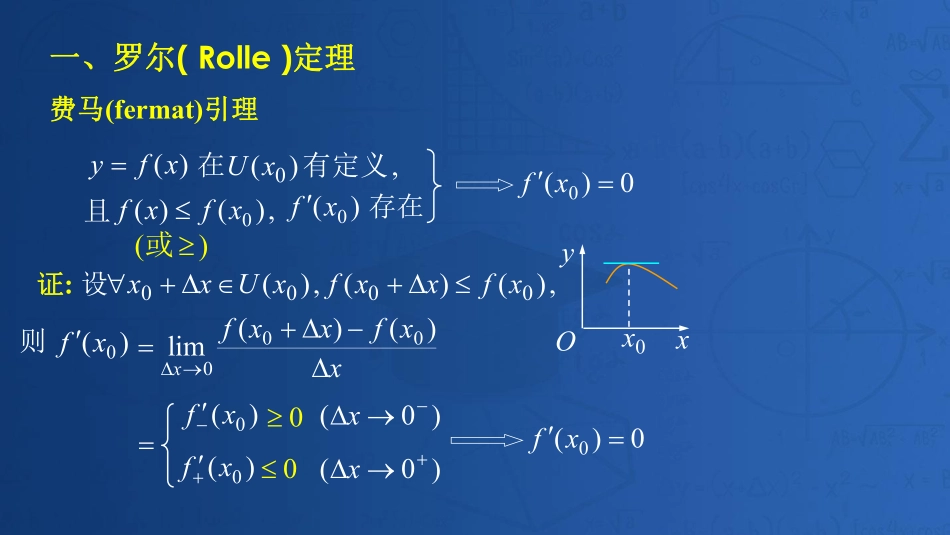
赵军高等数学零基础课程费马(fermat)引理一、罗尔(Rolle)定理,)(0有定义在xU且)(0xf存在,)()(0xfxf)(或0)(0xf证:设,)()(,)(0000xfxxfxUxx则)(0xfxxfxxfx)()(lim000)0(x)(0xf)0(x)(0xf000)(0xf)(xfyxyO0x罗尔（Rolle）定理)(xfy满足:(1)在区间[a,b]上连续(2)在区间(a,b)内可导(3)f(a)=f(b),使.0)(f在(a,b)内至少存在一点xyab)(xfyO例1.证明方程0155xx,15)(5xxxf.3)1(,1)0(ff,0)(0xf,,)1,0(011xxx)1(5)(4xxf),1,0(,0x有且仅有一个小于1的正实根.证:1)存在性.则)(xf在[0,1]连续,且由介值定理知存在,)1,0(0x使即方程有小于1的正根.0x2)唯一性.假设另有,0)(1xf使在以)(xf10,xx为端点的区间满足罗尔定理条件,之间在10,xx至少存在一点,.0)(f使但矛盾,故假设不真!设二、拉格朗日中值定理)((1)在区间[a,b]上连续)(xfy满足:(2)在区间(a,b)内可导至少存在一点,),(ba使.)()()(abafbff思路:利用逆向思维找出一个满足罗尔定理条件的函数作辅助函数显然,)(x在[a,b]上连续,在(a,b)内可导,且证:问题转化为证)(x)(xfxabafbf)()()(a由罗尔定理知至少存在一点,),(ba,0)(使即定理结论成立.,)(babbfaafb)()(0)()()(abafbff证毕xyab)(xfyOxyabafbf)()(推论:若函数在区间I上满足,0)(xf则)(xf在I上必为常数.)(xf证:在I上任取两点,)(,2121xxxx上用拉在],[21xx格朗日中值公式,得0)()(12xfxf))((12xxf)(21xx)()(12xfxf由的任意性知,21,xx)(xf在I上为常数.例2.证明等式.]1,1[,2πarccosarcsinxxx证:设,arccosarcsin)(xxxf上则在)1,1()(xf由推论可知Cxxxfarccosarcsin)((常数)令x=0,得.2πC又,2π)1(f故所证等式在定义域上成立.]1,1[211x211x0经验:欲证Ix时,)(0Cxf只需证在I上,0)(xf,0Ix且.)(00Cxf使例3.证明不等式证:设,)1ln()(ttf上满足拉格朗日在则],0[)(xtf中值定理条件,即因为故.)0()1ln(1xxxxx)0()(fxf)1ln(xxx0,11xxx1x)0()1ln(1xxxxxxxf0,)0)((因此应有例4.求)0()1arctan(arctanlim2ananann解利用中值定理求极限原式)1(11lim22nanann之间）与...