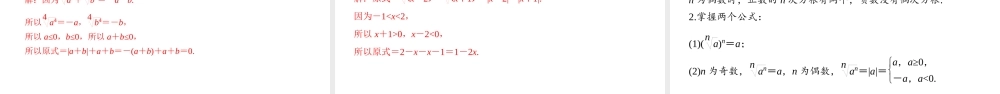4.1 第1课时 根式（课件）-2022-2023学年高一数学同步精品课堂（人教A版2019必修第一册）.pptxVIP免费

第四章指数函数与对数函数4.1指数第1课时根式学习目标素养目标学科素养1.理解n次方根及根式的概念，掌握根式的性质．(重点)2.能利用根式的性质对根式进行化简、运算．(重点、难点)1.数学抽象2.数学运算自主学习一．n次方根1.a的n次方根的定义一般地，如果，那么x叫做a的n次方根，其中n>1，且n∈N*.2.a的n次方根的表示n的奇偶性a的n次方根的表示符号a的取值范围n为奇数naa∈Rn为偶数±na[0，＋∞)xn＝a注意：负数没有偶次方根．自主学习二.n次根式1.根式：式子na叫做根式，这里n叫做，a叫做被开方数．2.根式的性质(1)n0＝(n∈N*，且n>1)；(2)(na)n＝(n∈N*，且n>1)；(3)nan＝(n为大于1的奇数)；(4)nan＝|a|＝a，a≥0，－a，a<0，(n为大于1的偶数)．根指数0aa自主学习思考：若x4＝3，这样的x有几个，如何表示？有2个，表示为±43.小试牛刀1.思辨解析(正确的打“√”，错误的打“×”)(1)任意实数的奇次方根只有一个．()(2)正数的偶次方根有两个且互为相反数．()(3)当n∈N*时，(n－2)n＝－2.()(4)π－42＝π－4.()2.m是实数，则下列式子中可能没有意义的是()A.4m2B．5mC.6mD．5－m√××√C解析：当m<0时，6m没有意义，其余各式均有意义．题型一根式的概念经典例题例1下列说法正确的个数是()①16的4次方根是2；②416的运算结果是±2；③当n为大于1的奇数时，na对任意a∈R都有意义；④当n为大于1的偶数时，na只有当a≥0时才有意义．A．1B．2C．3D．4B解析：①16的4次方根应是±2；②416＝2，所以正确的应为③④.题型一根式的概念经典例题总结n(n>1)次方根的个数及符号的确定：(1)正数的偶次方根有两个且互为相反数，任意实数的奇次方根只有一个．(2)根式na的符号由根指数n的奇偶性及被开方数a的符号共同确定：①当n为偶数时，na为非负实数；②当n为奇数时，na的符号与a的符号一致．跟踪训练1经典例题已知a∈R，n∈N*，给出下列4个式子：①6－32n；②5a2；③6－52n＋1；④9－a2，其中无意义的有()A．1个B．2个C．3个D．0个A解析：①中(－3)2n>0，所以6－32n有意义；②中根指数为5有意义；③中(－5)2n＋1<0，因此无意义；④中根指数为9，有意义．故选A.题型一根式的概念经典例题题型二利用根式的性质化简求值例2化简下列各式：(1)5－25＋(5－2)5；(2)6－26＋(62)6；(3)4x＋24.解：(1)原式＝(－2)＋(－2)＝－4.(2)原式＝|－2|＋2＝2＋2＝4.(3)原式＝|x＋2|＝x＋2，x≥－2，－x－2，x<－2.经典例题总结正确区...