3.2.2 函数的奇偶性-2022-2023学年高一数学教材配套教学精品课件（人教A版2019必修第一册).pptxVIP免费

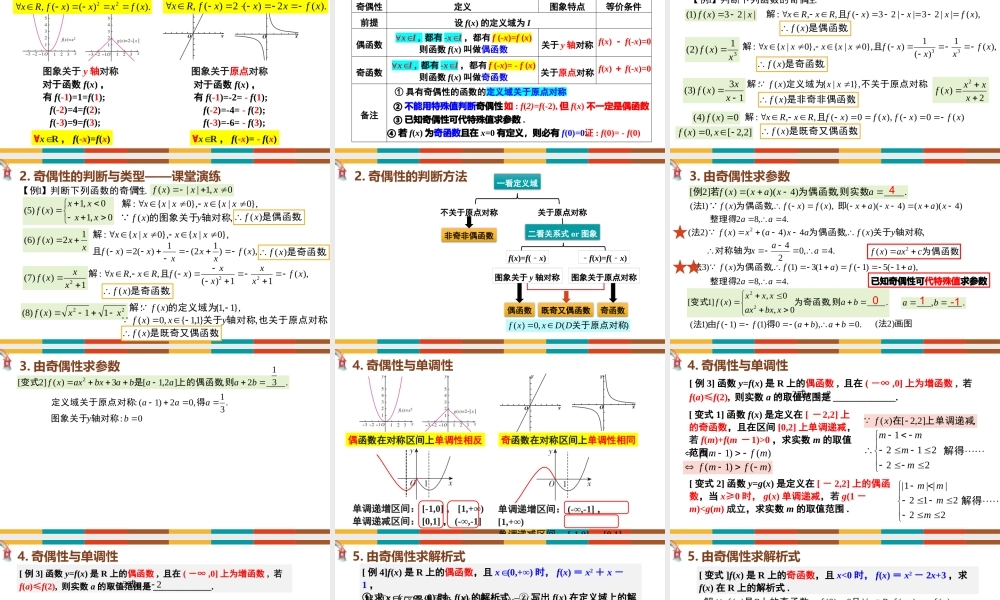
第三章函数的概念与性质3.2.2奇偶性Q1：观察下列两组函数图象各有什么特征？Q2：如何从代数的角度描述这一图象特征？图象关于y轴对称图象关于原点对称对于函数f(x)，有f(-1)=1=f(1);f(-2)=4=f(2);f(-3)=9=f(3);∀xR∈，f(-x)=f(x)对于函数f(x)，有f(-1)=-2=-f(1);f(-2)=-4=-f(2);f(-3)=-6=-f(3);∀xR∈，f(-x)=-f(x)).()()(,22xfxxxfRx).(2)(2)(,xfxxxfRx1.奇偶性的定义奇偶性定义图象特点等价条件前提设f(x)的定义域为I偶函数∀x∈I,都有-x∈I，都有f(-x)=f(x)则函数f(x)叫做偶函数关于y轴对称奇函数∀x∈I,都有-x∈I，都有f(-x)=-f(x)则函数f(x)叫做奇函数关于原点对称备注f(x)－f(-x)=0f(x)＋f(-x)=0①具有奇偶性的函数的定义域关于原点对称②不能用特殊值判断奇偶性.如:f(2)=f(-2),但f(x)不一定是偶函数③已知奇偶性可代特殊值求参数.④若f(x)为奇函数且在x=0有定义，则必有f(0)=0.证:f(0)=-f(0)2.奇偶性的判断与类型——例题讲解||23)()1(xxf),(||23||23)(,,:xfxxxfRxRx且解.)(是偶函数xf31)()2(xxf.)(是奇函数xf.1性】判断下列函数的奇偶【例),(1)(1)(},0|{},0|{:33xfxxxfxxxxxx且解.},1|{)(:不关于原点对称定义域为解xxxf.)(是既奇又偶函数xf13)()3(xxxf.)(是非奇非偶函数xf0)()4(xf)(0)(),(0)(,,:xfxfxfxfRxRx且解]2,2[,0)(xxf2)(2xxxxf2.奇偶性的判断与类型——课堂演练.1性】判断下列函数的奇偶【例,)(轴对称的图象关于 yxf0,10,1)()5(xxxxxf},1,1{)(:的定义域为解xf2211)()8(xxxf.,}1,1{,0)(也关于原点对称轴对称关于yxxf.)(是既奇又偶函数xfxxxf12)()6(},0|{},0|{:xxxxxx解),()12(1)(2)(xfxxxxxf且.)(是奇函数xf.)(是偶函数xf},0|{},0|{:xxxxxx解1)()7(2xxxf),(11)()(,,:22xfxxxxxfRxRx且解.)(是奇函数xf0,1||)(xxxf一看定义域二看关系式or图象不关于原点对称关于原点对称非奇非偶函数f(x)=f(﹣x)图象关于y轴对称﹣f(x)=f(﹣x)图象关于原点对称偶函数奇函数既奇又偶函数2.奇偶性的判断方法)(,0)(关于原点对称DDxxf3.由奇偶性求参数.____,)4)(()(]2[axaxxf则实数为偶函数若例),()(,)()1(xfxfxf为偶函数 法)4)(()4)((...