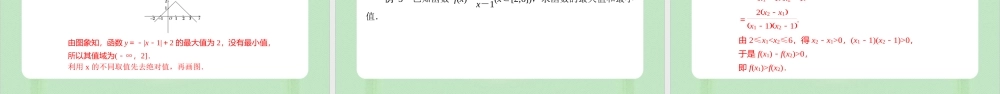第3章函数的概念与性质3.2.1单调性与最大(小)值人教A版2019高中数学必修第一册新课导入在初中我们利用函数图像探究过函数值随自变量的增大而增大(减小)的性质,这性质叫做函数的单调性.下面进一步刻画这种性质.先研究二次函数的单调性.画出图像,可以看到,当x<0时,y随x的增大而减小,也就是说,任意取,得到,有.这时我们就说函数在区间(-∞,0]上是单调递减的.同理,函数在[0,+∞)上是单调递增的.因为,所以【问题】如何判断本题中的大小?【1】观察图像法,从右侧图像中很容易得到函数在(-∞,0]上为减函数,在[0,+∞)上为增函数,但在(-∞,+∞)上不具有单调性.【2】做差法:所以单调性的定义一般地,设函数的定义域为S,区间,如果,当时,都有,那么就称函数在区间A上单调递增.特别地,若函数在它的定义域上单调递增时,我们就称它为增函数.如果,当时,都有,那么就称函数在区间A上单调递减.特别地,若函数在它的定义域上单调递减时,我们就称它为减函数.函数具有单调性的的区间叫做单调区间.函数单调性定义的等价形式(对于任意的):【1】在D上为增函数;【2】在D上为减函数;【3】在D上为增函数;【4】在D上为减函数.即自变量之差与函数值之差的乘积同号,函数为增函数;自变量之差与函数值之差的乘积同号,函数为减函数;单调性定义的应用【1】判断(证明)单调性:【2】比较函数值大小:【3】已知函数值大小比较自变量:【问题】书写函数的单调区间端点有何要求?函数在区间端点处有定义时,由于它的函数值是唯一确定的常数,没有增减的变化,所以不存在单调性问题,因此在书写单调区间时,可以包括,也可以不包括.如函数y=t的单调增区间可以写(0,+∞),也可以写成[0,+∞)反之,函数在区间端点处无定义时,书写单调区间时就不能包括端点.题型一利用函数图象求单调区间[经典例题]例1已知函数y=f(x)的图象如图所示,则该函数的减区间为()A.(-3,1)∪(1,4)B.(-5,-3)∪(-1,1)C.(-3,-1),(1,4)D.(-5,-3),(-1,1)单调性的应用【解析】在某个区间上,若函数y=f(x)的图象是上升的,则该区间为增区间,若是下降的,则该区间为减区间,故该函数的减区间为(-3,-1),(1,4).【答案】C观察图象,若图象呈上升(下降)趋势时为增(减)函数,对应的区间是增(减)区间.跟踪训练1函数f(x)的图象如图所示,则()A.函数f(x)在[-1,2]上是增函数B.函数f(x)在[-1,2]上是减函数C.函数f(x)在[-1,4]上是减函数D.函数f(x)在[2,4]上是增函数...