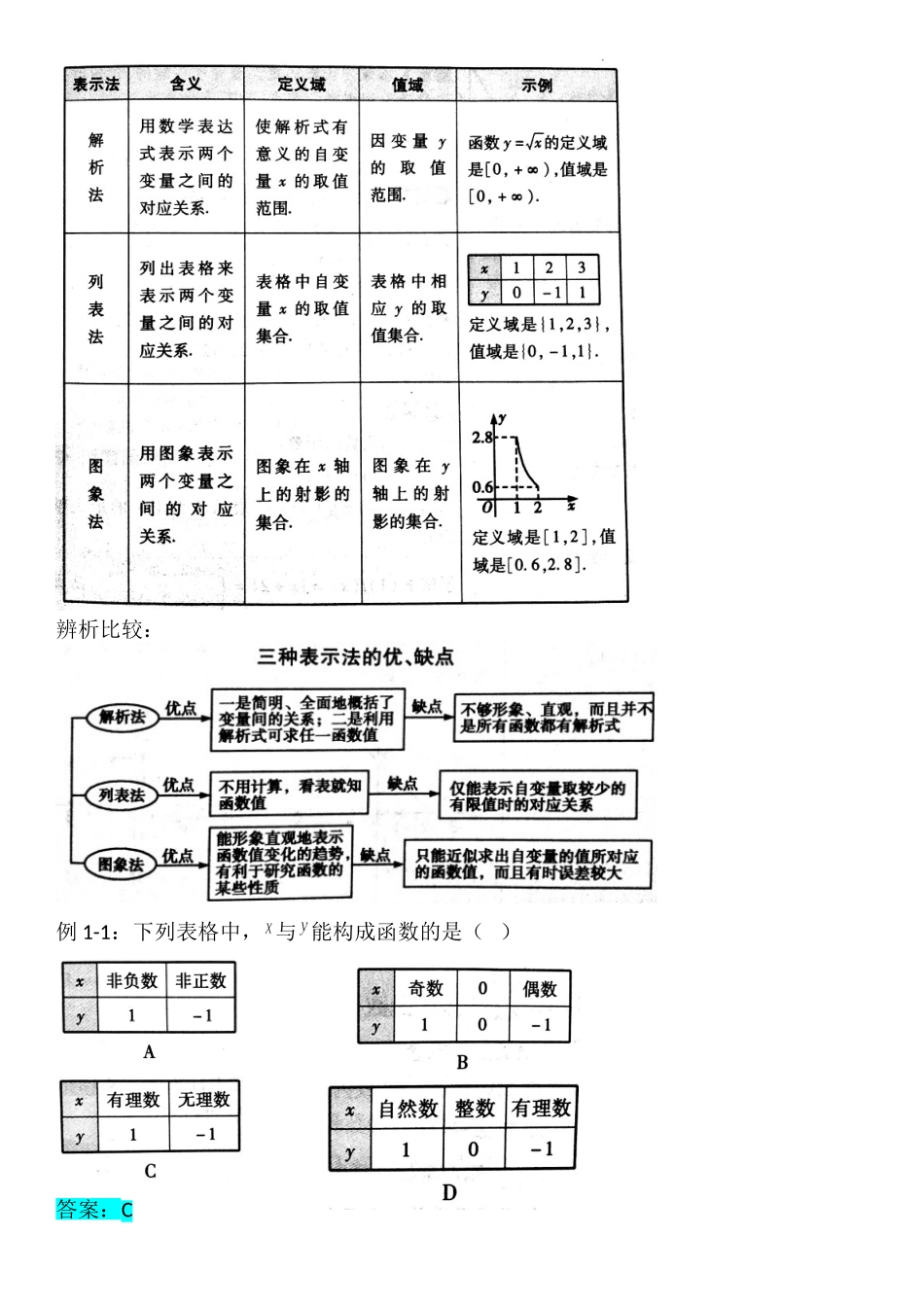
新教材必修第一册3.1.2:函数的表示方法课标解读:1.函数的表示方法(解析法、列表法、图像法)的概念及应用.(掌握)2.分段函数的概念及应用.(理解)学习指导:1.函数的三种表示体现了“式”“表”“图”互相结合,体现了数形结合的思想.学习过程中注意把“式”“表”“图”相互转化,特别注意加强“式”与“图”的互相转化,从侧面认识函数的本质.2.学习分段函数,要结合实例体会概念,还要注意书写的规范.知识导图:教材全解知识点1:函数的表示方法辨析比较:例1-1:下列表格中,与能构成函数的是()答案:C例1-2:已知完成某项任务的时间t与参加次项任务的人数之间适合关系式,当时,;当时,,且参加次项任务的人数不能超过20人.(1)写出函数的函数解析式;(2)用列表法表示此函数;(3)画出函数t的图像.答案:(1),;(2)略(3)略知识点2:分段函数1.分段函数的概念有些函数在其定义域内,对于自变量的不同取值区间,有着不同的对应关系,这样的函数称为分段函数。2.分段函数的图象分段函数有几段,它的图像就由几条曲线组成.在同一直角坐标系中,根据每段定义区间和表达式依次画图像,要注意每段图像的端点是空心点还是实心点,将每段图像组合到一起就得到整个分段函数的图象.例2-3:若,则()A.2B.3C.4D.5答案:C例2-4:画出下列函数图像:(1)(2)([]表示不大于的最大整数).答案:略重难拓展知识点3:函数的图象变换1.函数图像的平移变换函数的图像与函数及函数的图像有怎样的关系呢?我们先来看一个例子.作出函数的图像,观察它们之间有怎样的关系.在同一平面直角坐标系中,它们的图像如图所示:观察图像可知,函数的图像可以由函数的图像向左平移一个单位长度得到;函数的图像可以由函数的图像向下平移一个单位长度得到.由此得到如下规律:(1)函数的图像是由函数的图像沿轴向左或向右平移个单位长度得到,即“左加右减”;(2)函数的图像是由函数的图像沿轴向上或向下平移个单位长度得到,即“上加下减”;2.函数图像的对称变换函数的图像与函数,函数及函数的图象又有怎样的关系呢?我们来看一个例子.作出函数,,,的图像,观察它们之间有怎样的关系.在同一平面直角坐标系中作出①,②,③,④的图像的一部分,如图所示.观察图像可知:函数的图像可由函数的图像作轴的对称变换得到;函数的图像可由函数的图像作轴的对称变换得到;函数的图像可由函数的图像作关于原点的对称变换得到。由此可得如下规律.函数图像的对...