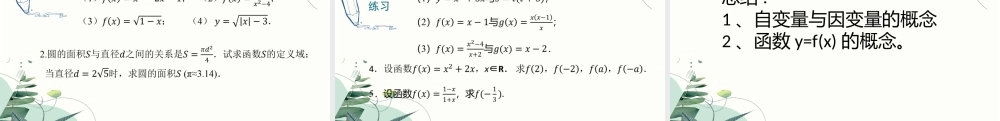3.1函数的概念学习目标:1、理解自变量与因变量的含义2、学会用集合与对应语言刻画函数概念3、会写出简单过程中的变量关系式。初中的函数:因变量y随自变量x的变化而变化的依赖关系。1、y=2x+12、y=-x2+2x-13、y=x3x是自变量(原因):在某一变化过程中,主动发生变化的量。y是因变量(结果):随着自变量的变化而发生变化的量。[函数的概念]设在一个变化过程中有两个变量x和y,集合A是一个非空的实数集,对于A内任意实数x,按照某一确定的法则f,都有唯一确定的实数y与它对应,这种对应关系叫做集合A上的一个函数,记作:函数概念包括:两个变量、对应关系;自变量的取值范围(即数集A)为这个函数的定义域f求平方123149记作:y=f(x),xA∈定义域:A={1,2,3}值域:{1,4,9}集合A值域例:写出下列各问题中的关乐式,并指出自变量与因变量:(1)圆的周长C与半径r的关系式:(1)C=2r,C是r的函数其中:r是自变量,C是因变量。(2)火车以90千米/小时的速度行驶,它驶过的路程S(千米)和所用时间t(小时)的关系式;(2)S=90t,S是t的函数其中:t是自变量,S是因变量。(3)一辆汽车要行驶50千米的路程,写出行驶时间t(小时)与行驶速度v(千米/小时)之间的关系式;(3)t是v的函数其中:v是自变量,堤因变量。vstvst例1求下列函数的定义域:情境导入探索新知例题辨析巩固练习归纳总结布置作业情境导入探索新知例题辨析巩固练习归纳总结布置作业例2判断下列函数是否为同一个函数,并说明理由.情境导入探索新知例题辨析巩固练习归纳总结布置作业练习情境导入探索新知例题辨析巩固练习归纳总结布置作业1.求下列函数的定义域:练习情境导入探索新知例题辨析巩固练习归纳总结布置作业3.判断下列各组函数是否为同一个函数,并说明理由.总结:1、自变量与因变量的概念2、函数y=f(x)的概念。