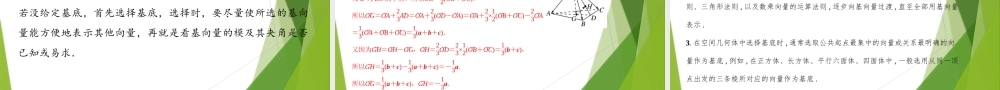1.2空间向量基本定理第1章空间向量与立体几何人教A版2019选修第一册01空间向量基底的概念及辨析02用空间基底表示向量03空间向量基本定理及其应用目录1.理解空间向量的正交分解,空间向量的基本定理;2.能用空间一个基底表示空间的任意向量.(重点)学习目标(1)定义:已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b.(2)数量积的运算律数乘向量与向量数量积的结合律(λa)·b=______交换律a·b=_____分配律a·(b+c)=_________a·b+a·cλ(a·b)b·a知识回顾(3)空间向量的夹角①定义:已知两个非零向量a,b,在空间任取一点O,作OA―→=a,OB―→=b,则______叫做向量a与b的夹角,记作〈a,b〉.②范围:〈a,b〉∈_______.特别地:当〈a,b〉=___时,a⊥b.∠AOB[0,π]π2知识回顾两个向量数量积的性质①若a,b是非零向量,则a⊥b⇔_______②若a与b同向,则a·b=______;若反向,则a·b=________.特别地,a·a=____或|a|=③若θ为a,b的夹角,则cosθ=_______a·aa·b|a||b|a·b=0|a|·|b|-|a|·|b||a|2知识回顾我们所在的教室即是一个三维立体图,如果以教室的一个墙角为始点,沿着三条墙缝作向量可以得到三个空间向量.这三个空间向量是不共面的,那么用这三个向量表示空间中任意的向量呢?我们知道平面内的任意一个向量都可以用两个不共线的向量来表示(平面向量基本定理),类似的任意一个空间的向量,能否用任意三个不共面的向量来表示呢?情景引入问题探究定理解析定理辨析1.空间任意三个不共面的向量都可构成空间的一个基底.基底选定后,空间的所有向量均可由基底唯一表示;不同基底下,同一向量的表达式也有可能不同.2.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.3.由于零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面,所以若三个向量不共面,就说明它们都不是零向量.思考1:基底选定后,空间中的所有向量均可由该基底唯一表示吗?不同基底下,同一个向量的表达式都相同吗?基底选定后,空间中的所有向量均可由该基底唯一表示,不一定相同,不同基底下,同一个向量的表达式也有可能不同.思考2:基底中能否有零向量?不能,因为零向量与任意一个非零向量共线,与任意两个非零向量共面.解读:1.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.2.基底的选择一般有两个条件:(1)基底必须是不共面的非零向量;(2)在进行基底...