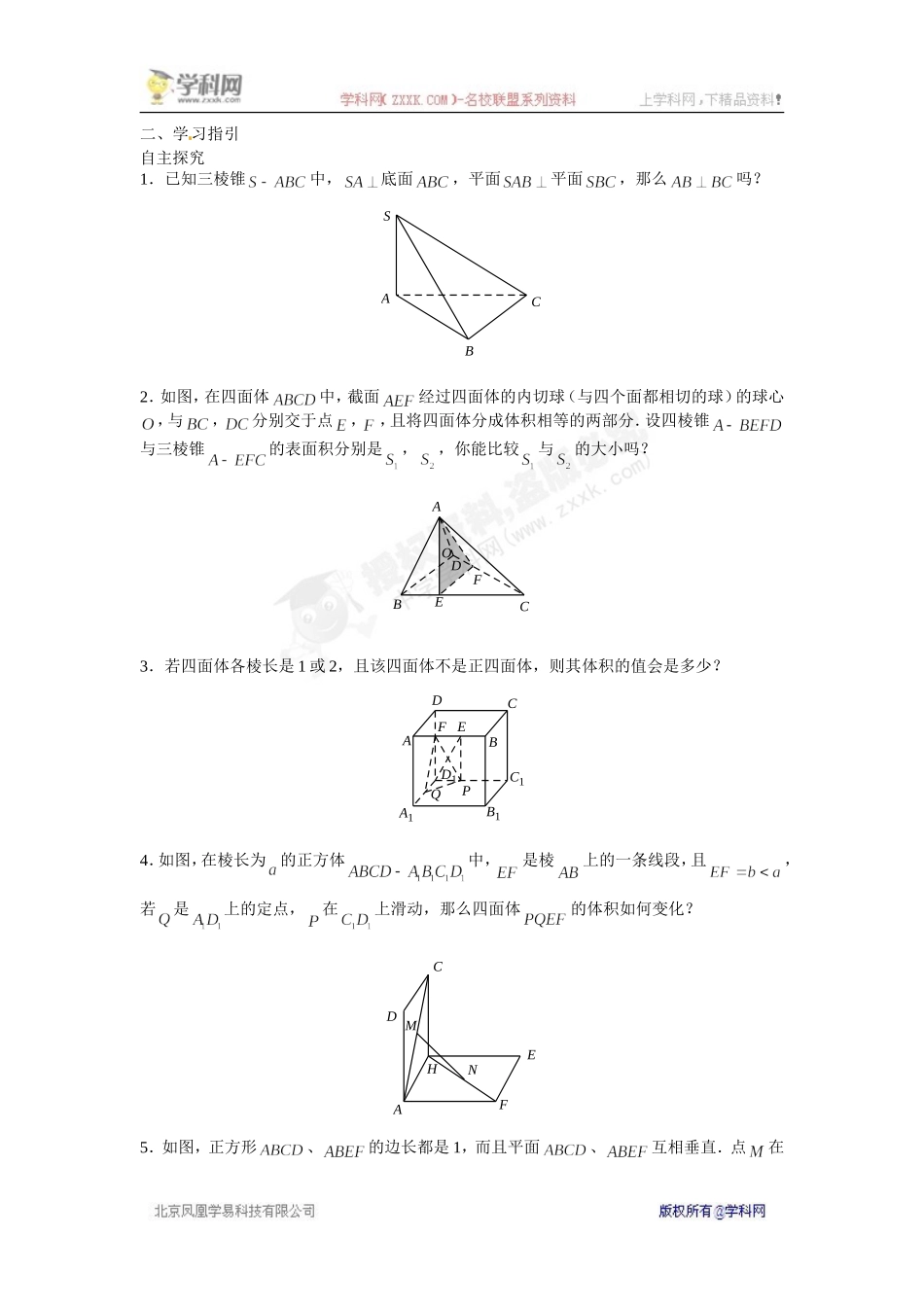
11.立体几何中的思想方法及其应用曾劲松学习目标1.熟练运用立体几何中常见的转化的思想方法:降维的转化、位置关系的转化、割补的转化、等积的转化等.2.熟练运用分类讨论的思想方法解决立体几何中的问题.[来源:学,科,网]3.能利用函数与方程的思想解决立体几何中的动态问题.4.进一步熟练解决以下基本题型:平行与垂直的证明、结论探索性问题、求空间角、求空间距离、翻折问题.一、夯实基础基础梳理1.立体几何中转化思想(1)降维的转化:由三维空间向二维平面转化,把空间的基本元素转化到某一个平面中去,用平面几何知识来解决问题.例如三种角(线线角、线面角、二面角)和四种距离(线线距、点面距、线面距、面面距)从定义到具体的计算都体现了空间到平面的转化.(2)位置关系的转化:空间平行关系之间的转化空间垂直关系之间的转化(3)割补的转化:通过“割”或“补”可化复杂图形为已熟知的简单几何体,从而较快地找到解决问题的突破口.例如有些特殊的三棱锥(或四棱锥),我们其放置在一个长方体中.(4)等体积的转化:求一个几何体的体积转化求另一个几何体的体积(或换一个角度求同一个几何体的体积).此法常用来求点到平面的距离,好处是回避了找垂足的具体位置.例如,求斜线与平面所成角时,只需求得斜线上某点到斜足的距离及该点到平面的距离,即可得到该角的正弦.2.熟练运用分类讨论的思想方法解决立体几何中的问题.例如【自主探究】第3题.3.能利用函数与方程的思想解决立体几何中的动态问题.动态问题是指某些点、线、面的位置是不确定的、可变的.我们可以考虑设置一个关键的变量,其它量的变化均由此变量引发,构建目标函数,于是用代数的方法来解决.要注意“动”与“静”是相对的,通常用一个特定的静的状态来研究运动中的几何体.4.翻折问题.把一个平面图形按照某种要求折起,转化为空间图形,进而研究图形在空间位置关系和数量上的变化,这就是翻折问题.这类题的关键是弄清翻折的变与不变,例如哪些角度、距离、位置关系发生了变化,而哪些没有.基础达标1.(2007年湖北)平面外有两条直线和,如果和在平面内的射影分别是和,给出下列四个命题:①;②;③与相交与相交或重合;④与平行与平行或重合.其中不正确命题的个数是().A.1B.2C.3D.42.(2010江西)过正方体的顶点作直线,使与棱所成的角都相等,这样的直线可以作().A.1条B.2条C.3条D.4条3.(2012年浙江)已知矩形,,.将沿矩...