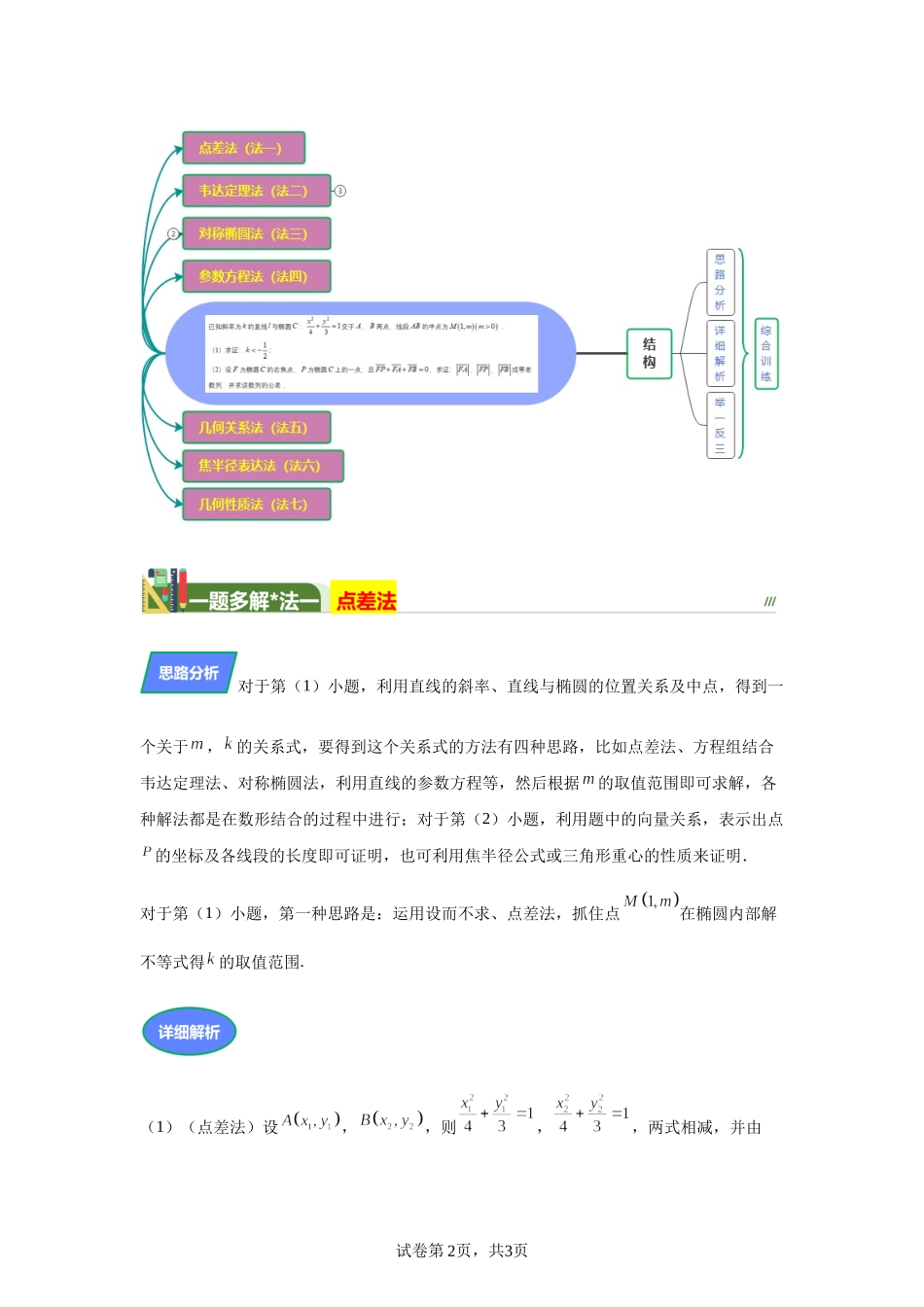
试卷第1页,共3页学科网(北京)股份有限公司第22题代数几何比翼齐飞,动静互变化难为易已知斜率为的直线与椭圆:交于,两点,线段的中点为.(1)求证:;(2)设为椭圆的右焦点,为椭圆上的一点,且,求证:,,成等差数列,并求该数列的公差.试卷第2页,共3页对于第(1)小题,利用直线的斜率、直线与椭圆的位置关系及中点,得到一个关于,的关系式,要得到这个关系式的方法有四种思路,比如点差法、方程组结合韦达定理法、对称椭圆法,利用直线的参数方程等,然后根据的取值范围即可求解,各种解法都是在数形结合的过程中进行;对于第(2)小题,利用题中的向量关系,表示出点的坐标及各线段的长度即可证明,也可利用焦半径公式或三角形重心的性质来证明.对于第(1)小题,第一种思路是:运用设而不求、点差法,抓住点在椭圆内部解不等式得的取值范围.(1)(点差法)设,,则,,两式相减,并由试卷第3页,共3页学科网(北京)股份有限公司得.由题设知,,于是.点在椭圆内部,可得,解得,故.(2023高三·全国·专题练习)1.已知椭圆C:,若椭圆C上有不同的两点关于直线对称,则实数m的取值范围是.对于第(1)小题,利用直线的斜率、直线与椭圆的位置关系及中点,得到一个关于,的关系式,要得到这个关系式的方法有四种思路,比如点差法、方程组结合韦达定理法、对称椭圆法,利用直线的参数方程等,然后根据的取值范围即可求解,各种解法都是在数形结合的过程中进行;对于第(2)小题,利用题中的向量关系,表示出点的坐标及各线段的长度即可证明,也可利用焦半径公式或三角形重心的性质来证明.对于第(1)小题,思路二是:联立直线方程和椭圆方程,消元运用韦达定理代入求得的取值范围,达到证明目的.(1)(韦达定理法)设的方程为,与椭圆联立,得.试卷第4页,共3页设,,则由,∴,①.②则,∴, ,∴或.由①②得,∴, ,∴.(23-24高三下·重庆·阶段练习)2.已知,动点满足与的斜率之积为定值.(1)求动点的轨迹的方程;(2)过点的直线与曲线交于两点,且均在轴右侧,过点作直线的垂线,垂足为.(i)求证:直线过定点;(ii)求面积的最小值.对于第(1)小题,利用直线的斜率、直线与椭圆的位置关系及中点,得到一个关于,的关系式,要得到这个关系式的方法有四种思路,比如点差法、方程组结合韦达定理法、对称椭圆法,利用直线的参数方程等,然后根据的取值范围即可求解,各种解法都是在数形结合的过程中进行;对于第(2)...