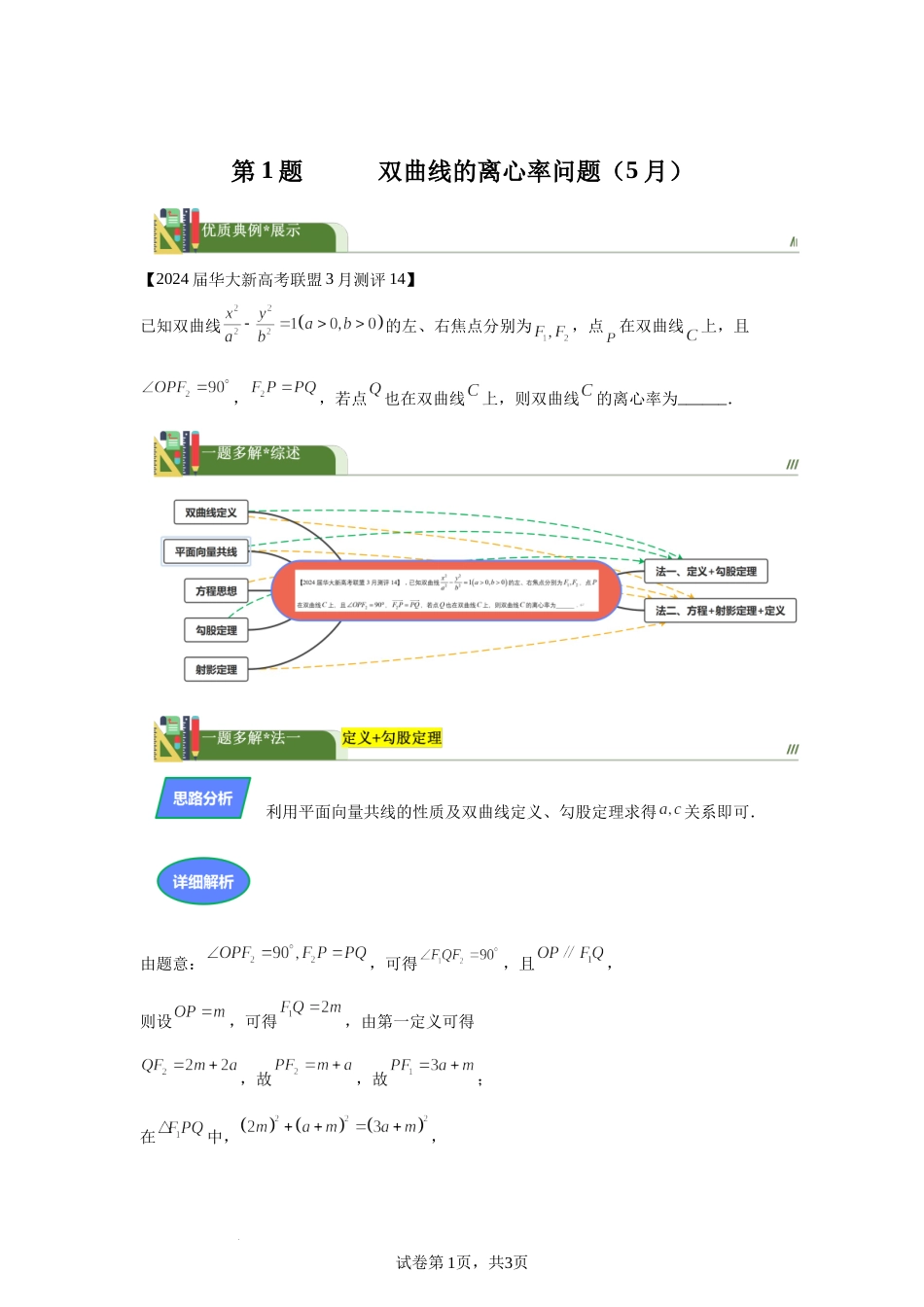
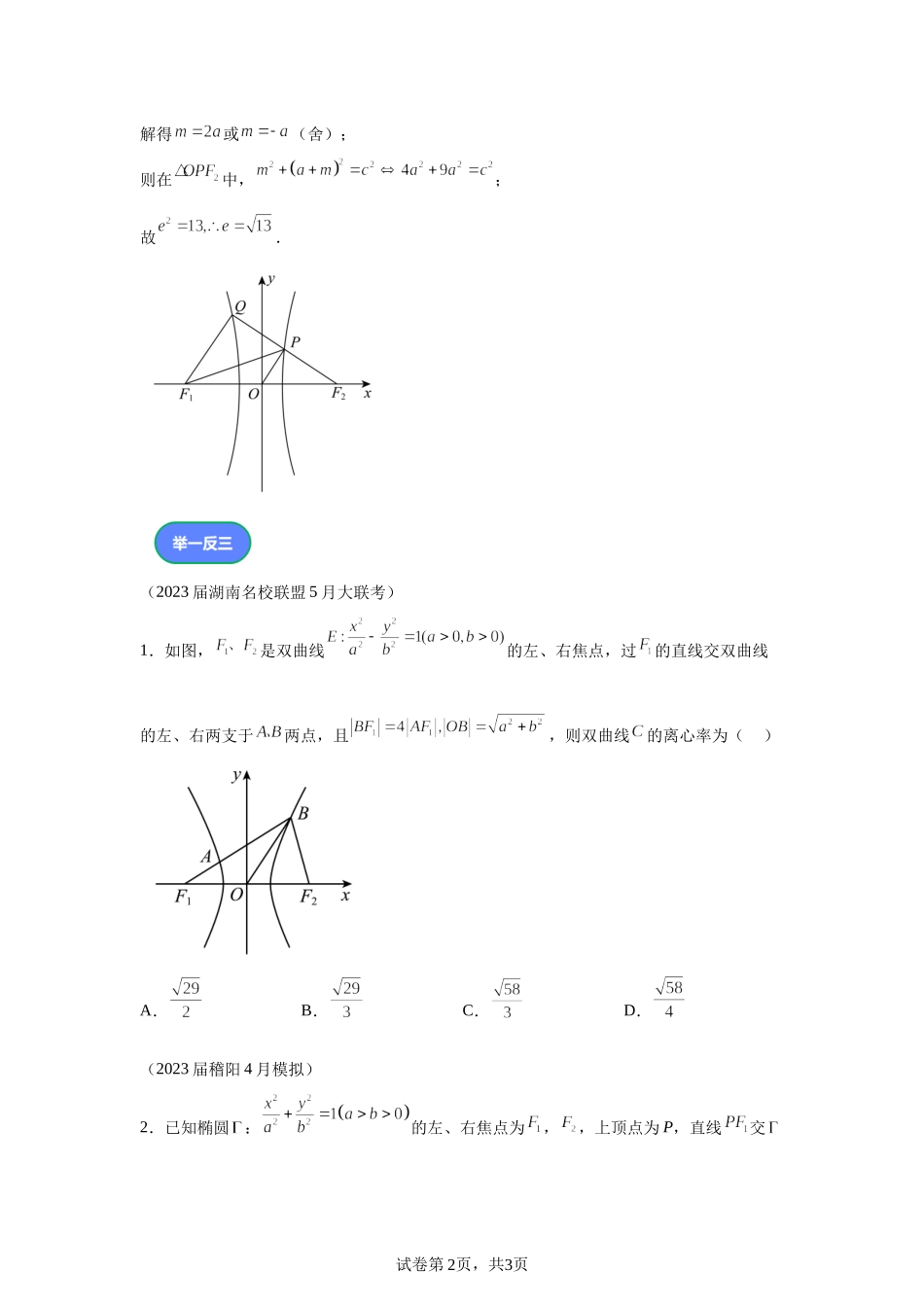
试卷第1页,共3页学科网(北京)股份有限公司第1题双曲线的离心率问题(5月)【2024届华大新高考联盟3月测评14】已知双曲线的左、右焦点分别为,点在双曲线上,且,,若点也在双曲线上,则双曲线的离心率为______.利用平面向量共线的性质及双曲线定义、勾股定理求得关系即可.由题意:,可得,且,则设,可得,由第一定义可得,故,故;在中,,试卷第2页,共3页解得或(舍);则在中,;故.(2023届湖南名校联盟5月大联考)1.如图,是双曲线的左、右焦点,过的直线交双曲线的左、右两支于两点,且,则双曲线的离心率为()A.B.C.D.(2023届稽阳4月模拟)2.已知椭圆:的左、右焦点为,,上顶点为P,直线交试卷第3页,共3页学科网(北京)股份有限公司于点Q,若,则椭圆的离心率是.设,由平面向量共线得坐标关系,根据点在双曲线上解方程可得P、Q横坐标,根据射影定理求得,利用,构造齐次式计算即可.设,由可得;将代入双曲线方程可得:,将代入可得,结合,可得;在中,由射影定理可得,;由,代入可得,化简可得,解得.试卷第4页,共3页(2024·浙江绍兴·二模)3.已知点A,B,C都在双曲线:上,且点A,B关于原点对称,.过A作垂直于x轴的直线分别交,于点M,N.若,则双曲线的离心率是()A.B.C.2D.(23-24高三下·天津·阶段练习)4.已知双曲线的左焦点为,过作渐近线的垂线,垂足为,且与抛物线交于点,若,则双曲线的离心率为()A.B.C.D.(2024·浙江台州·二模)5.设,是双曲线:的左、右焦点,点分别在双曲线的左、右两支上,且满足,,则双曲线的离心率为()A.2B.C.D.(2024·辽宁大连·一模)6.设是双曲线的左、右焦点,点A是双曲线C右支上一点,若的内切圆M的半径为a(M为圆心),且,使得,则双曲线C的离心率为()试卷第5页,共3页学科网(北京)股份有限公司A.B.C.2D.(2024·天津·一模)7.过双曲线的左焦点作圆的切线,切点为,直线交直线于点.若,则双曲线的离心率为()A.B.C.D.(2024·全国·一模)8.已知双曲线的左、右焦点分别为、,经过的直线交双曲线的左支于,,的内切圆的圆心为,的角平分线为交于M,且,若,则该双曲线的离心率是()A.B.C.D.2(23-24高三下·河南·阶段练习)9.已知双曲线的右焦点为F,过F作直线分别与双曲线的两渐近线相交于A,B两点,且,,则该双曲线的离心率为.(23-24高三下·江西鹰潭·阶段练习)10.已知双曲线:的左、右焦点分别为、点A在C上,点B...