8.2.4半角公式（课件）- 2020-2021学年高一下学期数学同步精品课堂(新教材人教B版2019 必修第三册).pptxVIP免费

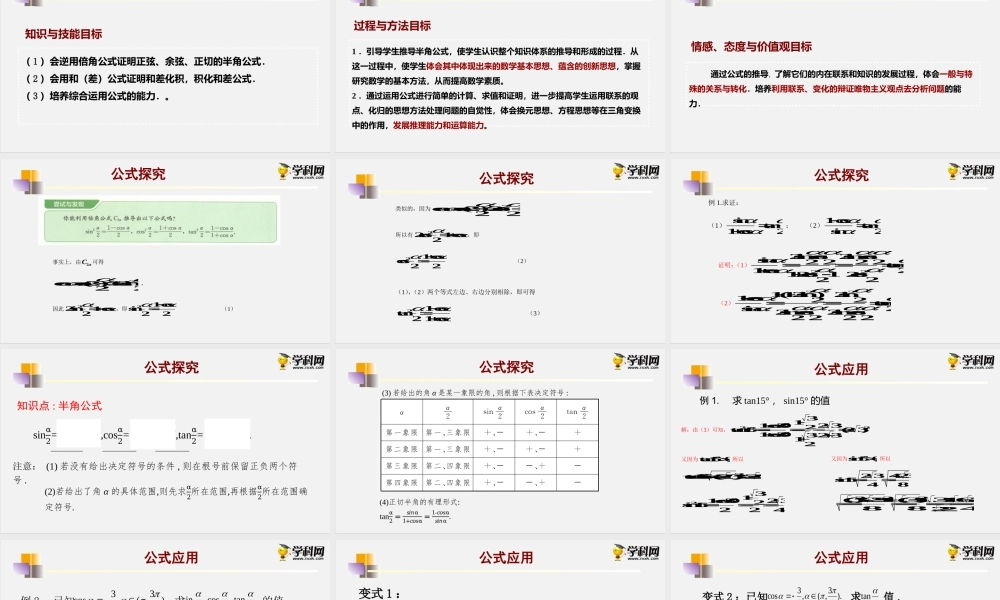
8.2.4半角公式数学（人教B版2019）必修第三册第八章向量的数量积与三角恒等变换学习目标（1）会逆用倍角公式证明正弦、余弦、正切的半角公式．（2）会用和（差）公式证明和差化积，积化和差公式．（3）培养综合运用公式的能力．。知识与技能目标1．引导学生推导半角公式，使学生认识整个知识体系的推导和形成的过程．从这一过程中，使学生体会其中体现出来的数学基本思想、蕴含的创新思想，掌握研究数学的基本方法，从而提高数学素质。2．通过运用公式进行简单的计算、求值和证明，进一步提高学生运用联系的观点、化归的思想方法处理问题的自觉性，体会换元思想、方程思想等在三角变换中的作用，发展推理能力和运算能力。过程与方法目标学习目标学习目标通过公式的推导，了解它们的内在联系和知识的发展过程，体会一般与特殊的关系与转化．培养利用联系、变化的辩证唯物主义观点去分析问题的能力．情感、态度与价值观目标公式探究事实上，由2C可得2coscos(2)12sin22，因此22sin1cos2，即21cossin22（1）公式探究类似的，因为2coscos(2)2cos122所以有22cos1cos2，即21coscos22（2）（1），（2）两个等式左边、右边分别相除，即可得21costan21cos（3）公式探究例1.求证：（1）sintan1cos2；（2）1costansin2证明：（1）222sincos2sincossin2222tan1cos212cos12cos22（2）221(12sin)2sin1cos22tansin22sincos2sincos2222公式探究知识点:半角公式sinα2=±ට1-𝑐𝑜𝑠α2,cosα2=±ට1+𝑐𝑜𝑠α2,tanα2=±ට1-𝑐𝑜𝑠α1+𝑐𝑜𝑠α.注意：(1)若没有给出决定符号的条件,则在根号前保留正负两个符号.(2)若给出了角α的具体范围,则先求α2所在范围,再根据α2所在范围确定符号.公式探究(3)若给出的角α是某一象限的角,则根据下表决定符号:(4)正切半角的有理形式:tanα2=𝑠𝑖𝑛α1+𝑐𝑜𝑠α=1-𝑐𝑜𝑠α𝑠𝑖𝑛α.公式应用例1.求tan15°，sin15°的值解：由（3）可知，22311cos30232tan15=(23)1cos303231+2ooo又因为tan150,o所以2tan15(23)23o2311cos30232sin15224o又因为sin150,o所以23423sin1548222(3)231(31)316288422公式应用).23,(,53cos2tan,2cos,2sin例2：已知求的值.2（1）欲求的三角函数...