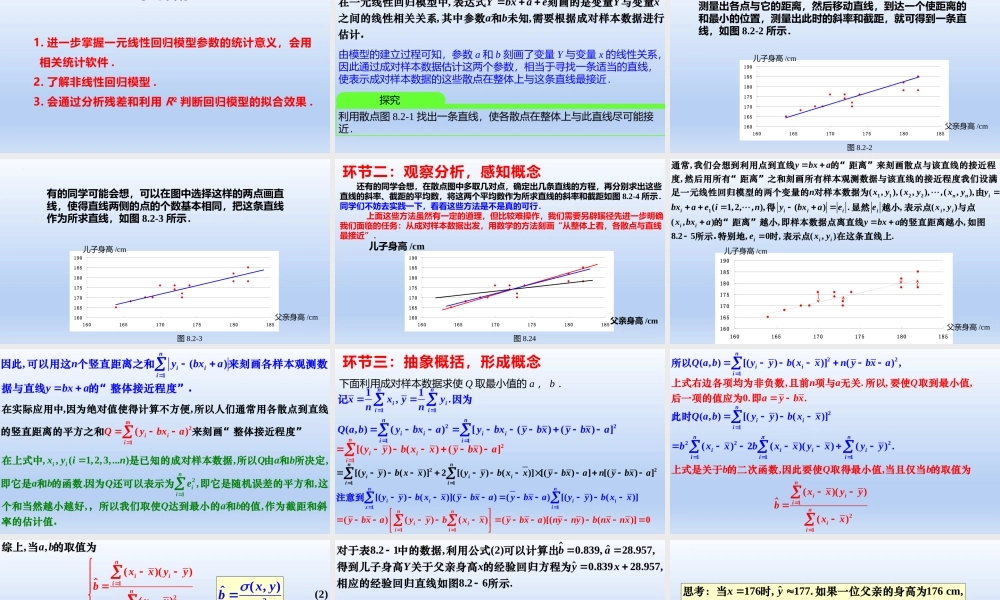
人教A版2019选择性必修第三册1.进一步掌握一元线性回归模型参数的统计意义,会用相关统计软件.2.了解非线性回归模型.3.会通过分析残差和利用R2判断回归模型的拟合效果.学习目标,,,YbxaYxaeb在一元线性回归模型中表达式刻画的是变量与变量之间的线性相关关系其中参数和未知需要根据成对样本数据进行估计.由模型的建立过程可知,参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.探究利用散点图8.2-1找出一条直线,使各散点在整体上与此直线尽可能接近.环节一:创设情境,引入课题160165170175180185190160165170175180185儿子身高/cm父亲身高/cm图8.2-2有的同学可能会想,可以采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距,就可得到一条直线,如图8.2-2所示.160165170175180185190160165170175180185儿子身高/cm父亲身高/cm图8.2-3有的同学可能会想,可以在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同,把这条直线作为所求直线,如图8.2-3所示.160165170175180185190160165170175180185儿子身高/cm父亲身高/cm图8.24还有的同学会想,在散点图中多取几对点,确定出几条直线的方程,再分别求出这些直线的斜率、截距的平均数,将这两个平均数作为所求直线的斜率和截距如图8.2-4所示.同学们不妨去实践一下,看看这些方法是不是真的可行.上面这些方法虽然有一定的道理,但比较难操作,我们需要另辟蹊径先进一步明确我们面临的任务:从成对样本数据出发,用数学的方法刻画“从整体上看,各散点与直线最接近”.环节二:观察分析,感知概念160165170175180185190160165170175180185儿子身高/cm父亲身高/cm11221,(,),(,),,(,),(1,,.2,,),(),(,),(),iiinniiiiiiinxyxyxyybxaeinybxaeexyxybxabxa通常的“距离我们会想到利用点到直线来刻画散点与该直线的接近程度然后用所有之和刻画所有样本观测数据与该直线的接近程度我们设满足一元线性回归模型的两个变量的对样”本数据为由“距离”显然的“距离得越小表示点与”越小点即样,8.25,0,(,).iiiybxaexy本数据点离直线的竖直距离越小如图所示.特别地时表示点在这条直线上1,()niiinybxaybxa因此可以用这个竖直距离之和来刻画各样本观测数据...