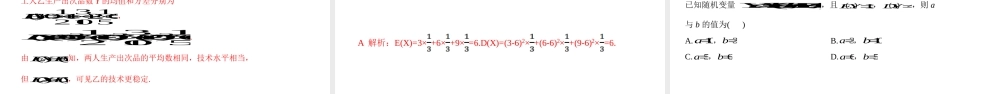7.3.2 离散型随机变量的方差（课件）-2021-2022学年高二数学教材配套学案+课件+练习（人教A版2019选择性必修第三册）.pptxVIP免费

7.3离散型随机变量的数字特征7.3.2离散型随机变量的方差课程标准素养目标理解离散型随机变量的方差.1.理解离散型随机变量的方差及标准差的概念.(数学抽象)2.掌握方差的性质,会利用公式求离散型随机变量的方差.(数学运算)3.会计算离散型随机变量的方差,并能解决一些实际问题.(数学建模、数学运算)学习目标自主学习一、离散型随机变量的方差、标准差：设离散型随机变量X的分布列为Xx1x2…xi…xnPp1p2…pi…pn则(xi－E(X))2描述了xi(i＝1,2，…，n)相对于均值E(X)的偏离程度，所以为这些偏离程度的加权平均，刻画了随机变量X与其均值E(X)的平均偏离程度．我们称D(X)为随机变量X的，并称其算术平方根为随机变量X的．21()()niiiDXxEXp221(())niiixpEX方差标准差自主学习思考：离散型随机变量的方差和样本方差之间有何关系?(1)离散型随机变量的方差即为总体的方差,它是一个常数,不随样本的变化而变化;(2)样本方差则是随机变量,它是随样本不同而变化的.自主学习二、离散型随机变量方差的性质：设a,b,c为常数，则(1)D(c)＝0;(2)()()DXbDX;(3)2()()DaXaDX;(4)2()()DaXaDX.自主学习三、服从两点分布与二项分布的随机变量的方差：(1)若X服从两点分布，则D(X)＝(其中p为成功概率)；(2)若X～B(n，p)，则D(X)＝.p(1-p)np(1-p)小试牛刀1.思维辨析(对的打“√”,错的打“×”)(1)离散型随机变量的方差越大,随机变量越稳定.()(2)离散型随机变量的方差与标准差的单位是相同的.()(3)若a是常数,则D(a)=0.()××√小试牛刀2.已知X的分布列为X-101P0.50.30.2则D(X)等于()A.0.7B.0.61C.-0.3D.0B解析：E(X)=-1×0.5+0×0.3+1×0.2=-0.3,D(X)=0.5×(-1+0.3)2+0.3×(0+0.3)2+0.2×(1+0.3)2=0.61.题型一方差、标准差的概念及性质经典例题例1已知X的分布列如表:X-101Pa(1)计算X的方差;(2)若Y=4X+3,求Y的均值和方差.经典例题解：由分布列的性质,知++a=1,故a=.所以X的均值E(X)=(-1)×+0×+1×=-.(1)X的方差D(X)=×+×+×=.(2)因为Y=4X+3,所以E(Y)=4E(X)+3=2,D(Y)=42D(X)=11.题型一方差、标准差的概念及性质经典例题跟踪训练1已知随机变量X的分布列如下表，且2EX，则p_____，23DX______.X12aP16p1312；4解析：由题意得，11163p，12p.由期望公式得111()022623EXa，3a.222111()(02)(22)(32)1623DX.故22324DXDX.题型一方差、标准差的概念及性质题型二求离散型随机变...