7.3.2离散型随机变量的方差 课件-2022-2023学年高二下学期数学人教A版（2019）选择性必修第三册.pptxVIP免费

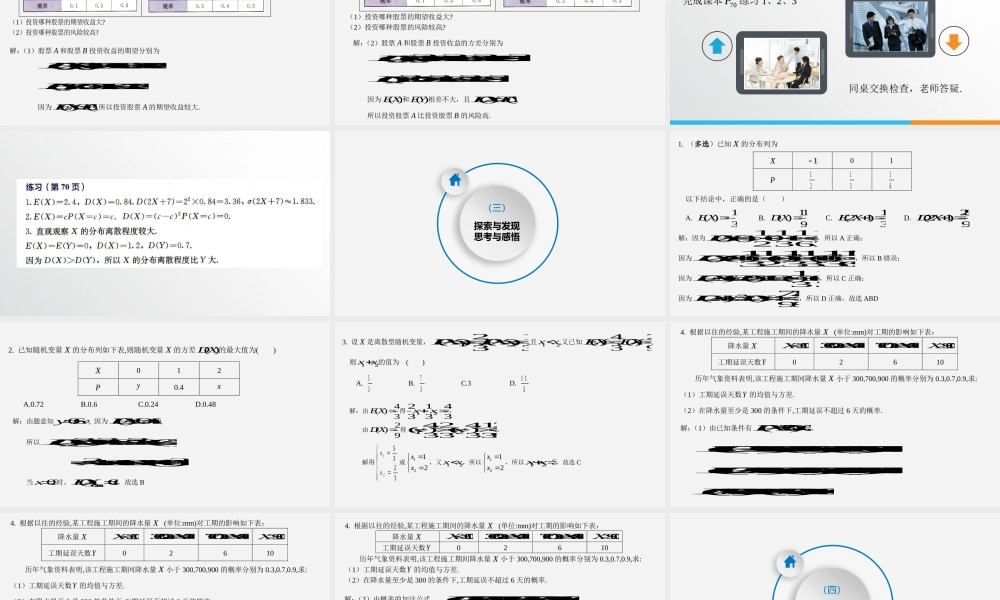
7.3.2离散型随机变量的方差第七章随机变量及其分布凯里一中尹洪January26,2025（一）创设情境揭示课题【回顾】随机变量的均值或数学期望一般地，若离散型随机变量X的分布列如下表所示，则称11221()..nnniiiEXxpxpxpxp为随机变量X的均值(mean)或数学期望(mathematicalexpectation),数学期望简称期望.()()EaXbaEXb【情景一】有A，B两种不同品牌的手表，它们的“日走时误差”分别为X，Y（单位：s），X，Y的分布列如下：品牌A品牌BX0.010.000.01P131313Y0.500.000.50P131313（1）分别计算X，Y的均值，并进行比较；（2）这两个随机变量的分布有什么不同，如何刻画这种不同？【解析】（1）111()0.010.000.010333EX111()0.500.000.500333EY所以这两种表的平均日走时误差都是0，因此仅仅根据平均误差，不能判断出哪一种品牌的表更好.（2）观察发现A品牌的表的误差只有±0.01s，而B品牌的表的误差为±0.05s，所以A品牌的表要好一些.【问题】除了均值外，还有其他刻画随机变量特点的指标吗？【阅读研讨】研读课本6769PP，交流记忆相关结论（用时约3-5分钟）（二）阅读精要研讨新知【思考】怎样定量刻画离散型随机变量取值的离散程度?【解读】随机变量的方差(variance)与标准差(standarddeviation)设离散型随机变量X的分布列如下表所示.方差2221122()(())(())...(())nnDXxEXpxEXpxEXp21(())niiixEXp，有时也记为()VarX.标准差()DX，记为()X.【探究与发现】（1）方差的简化运算：22121()(()()())niiiiniixEXDXxpEpX（2）随机变量aXb与X的方差关系：随机变量的方差的性质()()DXbDX2()()DaXaDX2()()DaXbaDX例题研讨学习例题的正规表达学习例题的常规方法从例题中学会思考如何看例题阅读领悟课本69P例5、例6例5抛掷一枚质地均匀的骰子，求掷出的点数X的方差.解：随机变量X的分布列为1(),1,2,3,4,5,66PXkk因为62222222171191(),()(123456)2666kEXk所以62211735()()()6212kDXk例6投资,AB两种股票，每股收益的分布列分别如表7.3-9和表7.310所示.（1）投资哪种股票的期望收益大?（2）投资哪种股票的风险较高?解：（1）股票A和股票B投资收益的期望分别为()(1)0.100.320.61.1EX()00.310.420.31EY因为()()EXEY,所以投资股票A的期望收益较大.例6投资,AB两种股票，每股收益的分...