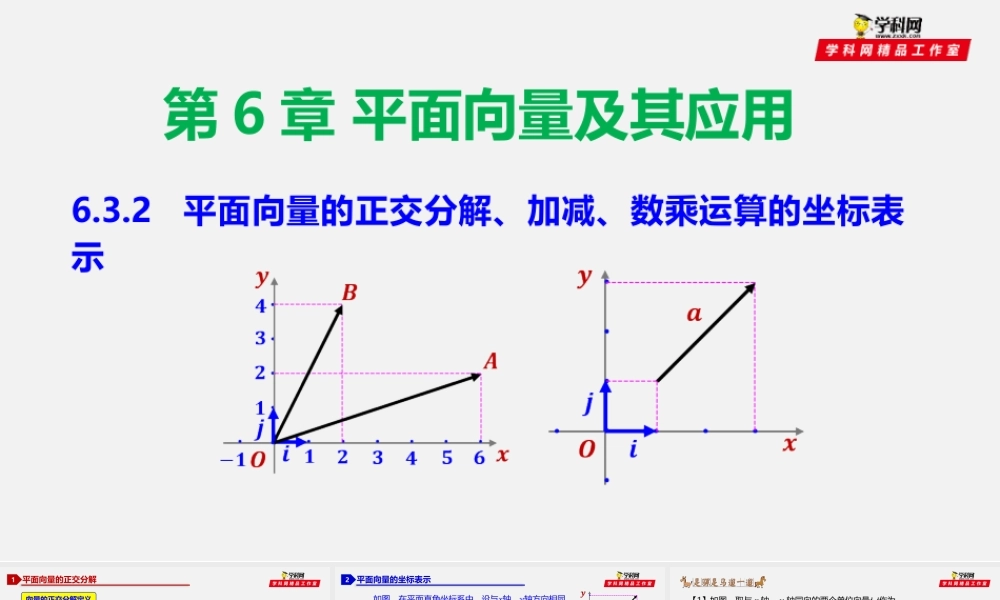
第6章平面向量及其应用6.3.2平面向量的正交分解、加减、数乘运算的坐标表示平面向量的正交分解1向量的正交分解定义把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.正交分解可看成是平面向量基本定理的特例,平面向量的基本定理是把平面内的任意一个向量分解为两个不共线的向量,正交分解则是这两个不共线向量互相垂直的特殊形式.在不共线的两个向量中,垂直是一种特殊的情形,向量的正交分解是向量分解常用且重要的一种分解.在平面上,如果选取互相垂直的向量作为基底,会大大方便我们解决问题.平面向量的坐标表示2···············【解】由题目所给的图可得········所以它们的坐标表示分别是:平面向量的坐标表示2高阶笔记向量的坐标表示是继向量的几何表示、字母表示后的又一种表示方法,向量的坐标表示实际上是向量的代数表示平面向量的坐标表示2点的坐标与向量的关系·····这样,我们就建立了向量的坐标与点的坐标之间的联系.平面向量的坐标表示2——点的坐标与向量的坐标的联系和区别辨析点的坐标反映的是点的位置,而向量的坐标反映的是向量的大小和方向.向量的坐标仅仅由向量的大小和方向决定,与向量的位置无关.联系①当且仅当向量的起点为原点时,向量终点的坐标等于向量本身的坐标.注意相等向量的坐标是相同的,但是两个相等向量的起点、终点的坐标却可以不同.区别平面向量的坐标运算3两个向量的和(差)的坐标分别等于这两个向量相应坐标的和(差)两个向量和(差)的坐标表示任一向量的坐标因此,一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标求一个点的坐标,可以转化为求以坐标原点为起点,以该点为终点的有向线段表示的向量的坐标平面向量的坐标运算3重点笔记在求一个向量的坐标时,可以首先求出表示这个向量的有向线段的起点坐标和终点坐标,再用终点的坐标减去起点的坐标从而得到该向量的坐标向量的坐标只与表示此向量的有向线段的起点、终点的相对位置有关,而与他们的具体位置无关.当向量确定以后,向量的坐标就是唯一确定的,因此向量在平移前后,坐标不变.平面向量共线的坐标表示4重点笔记特殊情况拓展平面向量共线的坐标表示4归纳与总结三点共线的坐标表示5引进向量的坐标表示后,向量的线性运算可以通过坐标来实现,三点共线问题也可以通过平面向量共线的坐标表示来判定.两种方法的本质都是向量共线定理(2)任取三点构成向量,计算出两向量如AB,AC,再通过两向量共线的...