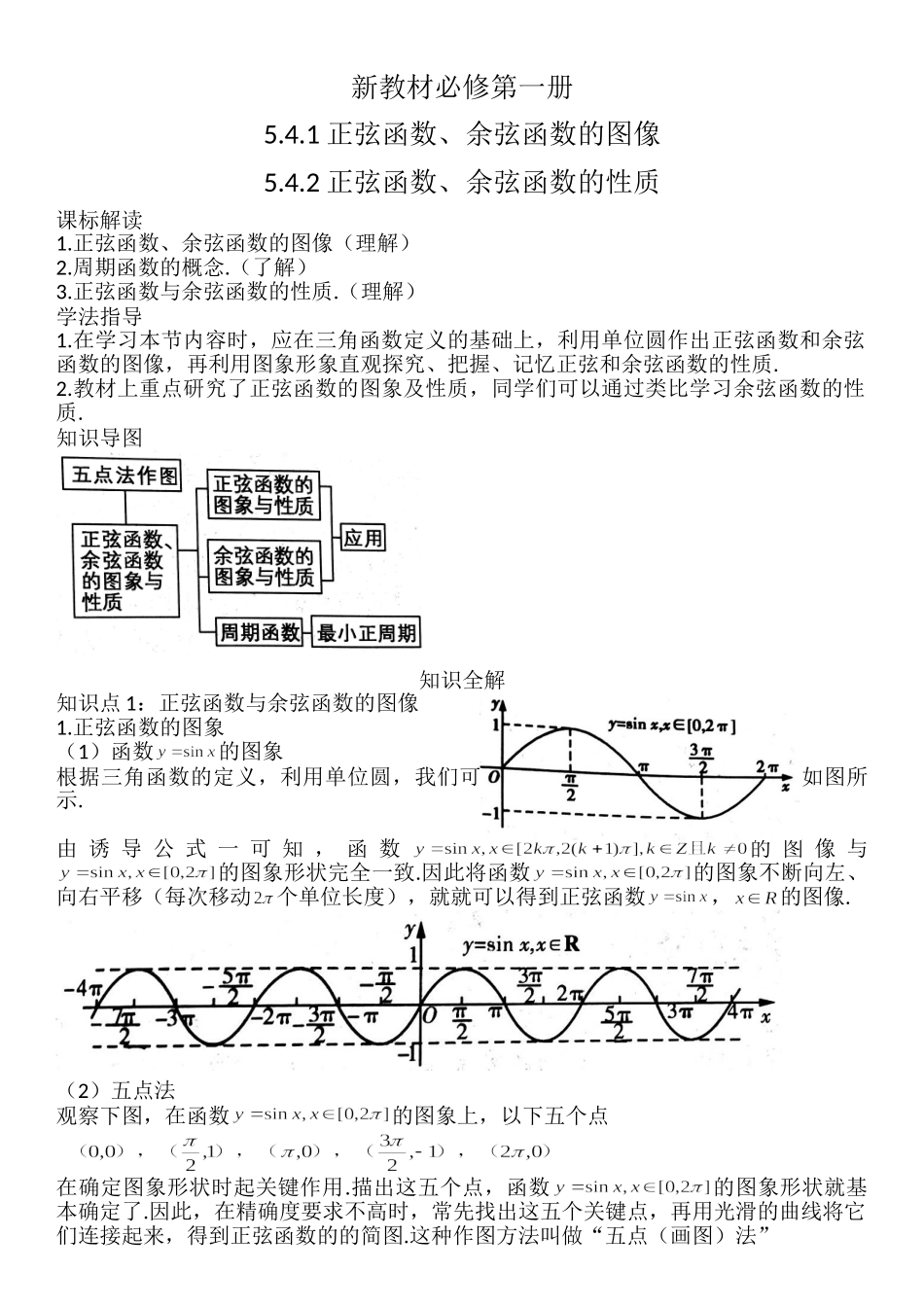
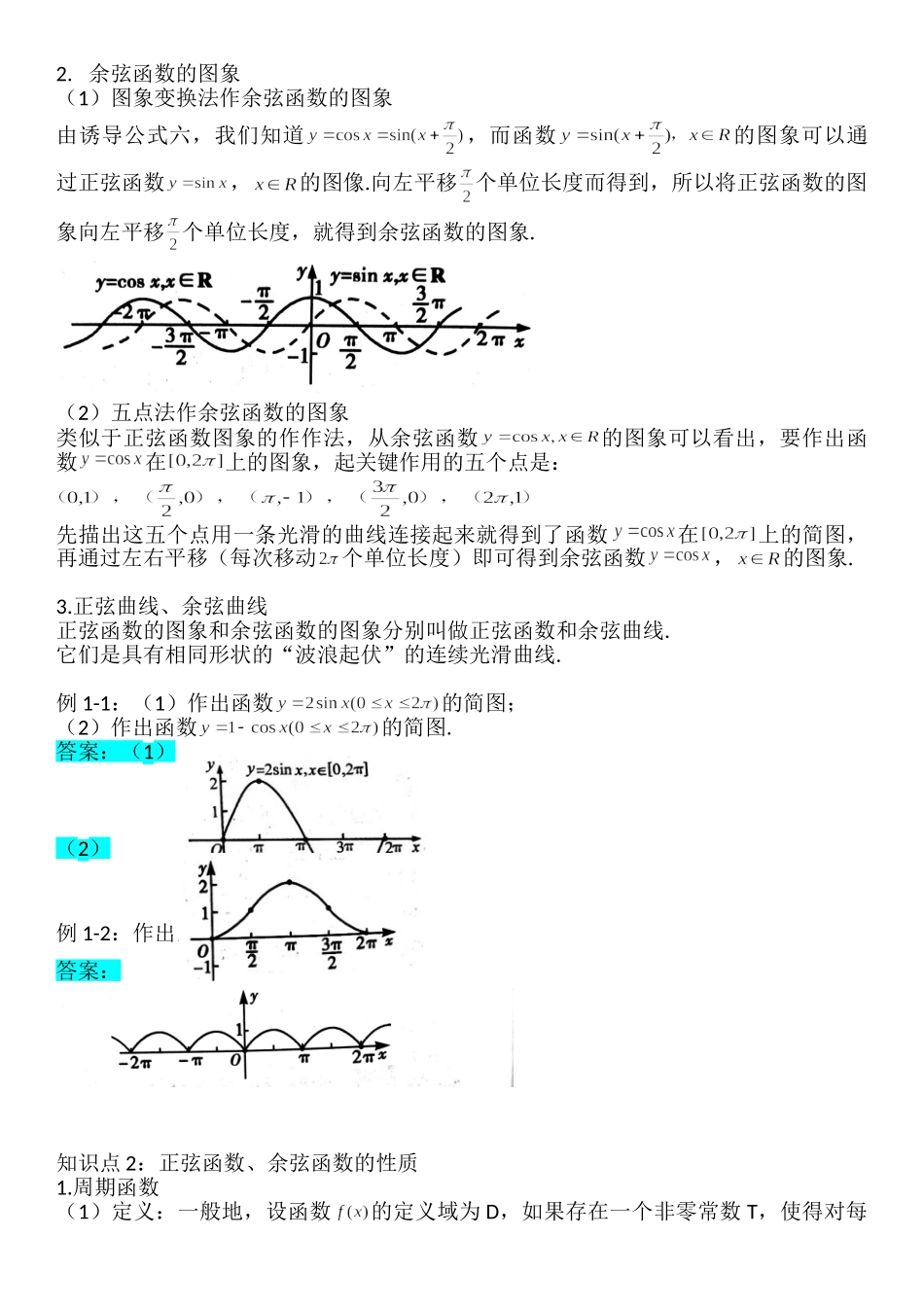
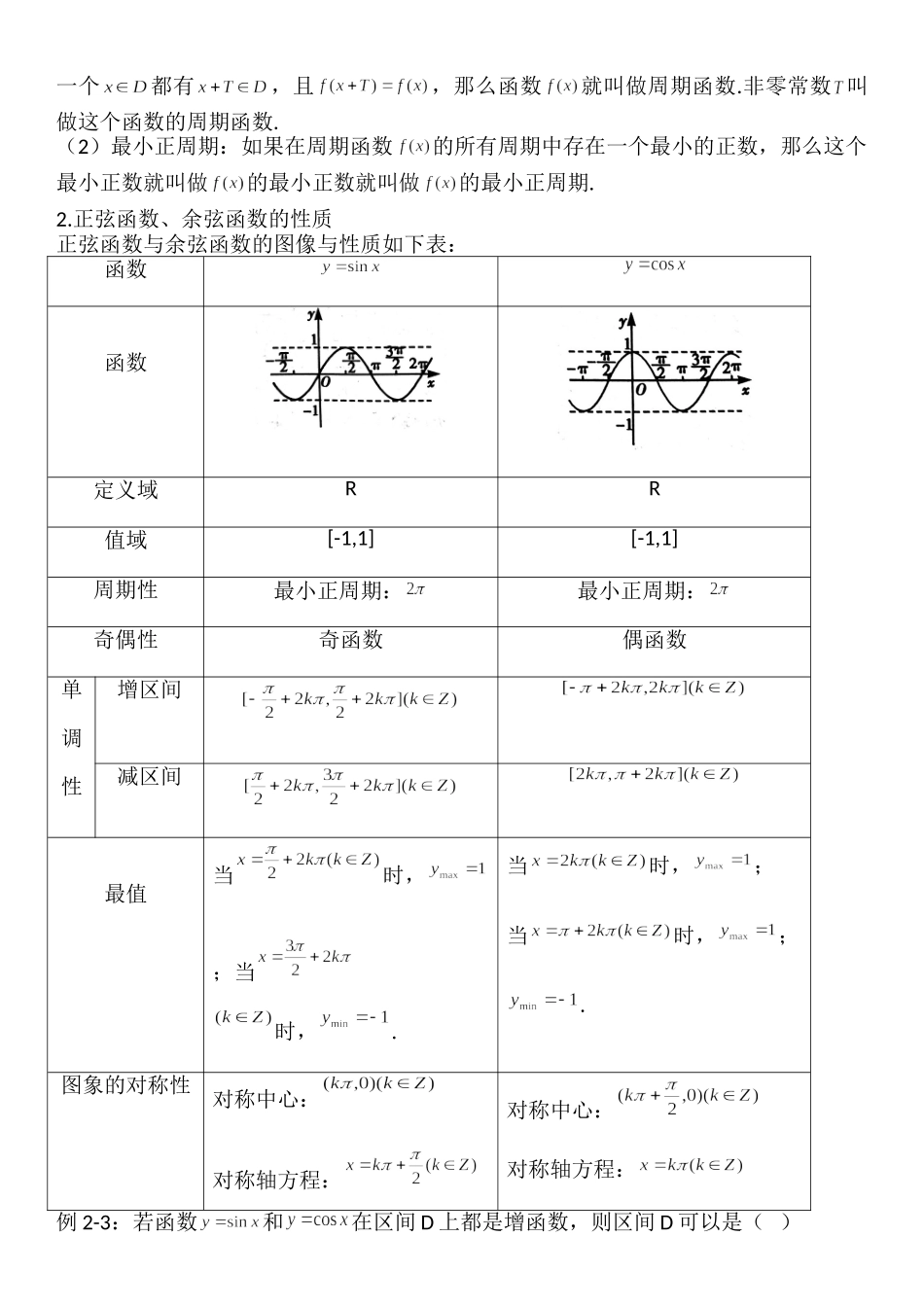
新教材必修第一册5.4.1正弦函数、余弦函数的图像5.4.2正弦函数、余弦函数的性质课标解读1.正弦函数、余弦函数的图像(理解)2.周期函数的概念.(了解)3.正弦函数与余弦函数的性质.(理解)学法指导1.在学习本节内容时,应在三角函数定义的基础上,利用单位圆作出正弦函数和余弦函数的图像,再利用图象形象直观探究、把握、记忆正弦和余弦函数的性质.2.教材上重点研究了正弦函数的图象及性质,同学们可以通过类比学习余弦函数的性质.知识导图知识全解知识点1:正弦函数与余弦函数的图像1.正弦函数的图象(1)函数的图象根据三角函数的定义,利用单位圆,我们可以得到的图象,如图所示.由诱导公式一可知,函数的图像与的图象形状完全一致.因此将函数的图象不断向左、向右平移(每次移动个单位长度),就就可以得到正弦函数,的图像.(2)五点法观察下图,在函数的图象上,以下五个点在确定图象形状时起关键作用.描出这五个点,函数的图象形状就基本确定了.因此,在精确度要求不高时,常先找出这五个关键点,再用光滑的曲线将它们连接起来,得到正弦函数的的简图.这种作图方法叫做“五点(画图)法”2.余弦函数的图象(1)图象变换法作余弦函数的图象由诱导公式六,我们知道,而函数的图象可以通过正弦函数,的图像.向左平移个单位长度而得到,所以将正弦函数的图象向左平移个单位长度,就得到余弦函数的图象.(2)五点法作余弦函数的图象类似于正弦函数图象的作作法,从余弦函数的图象可以看出,要作出函数在上的图象,起关键作用的五个点是:先描出这五个点用一条光滑的曲线连接起来就得到了函数在上的简图,再通过左右平移(每次移动个单位长度)即可得到余弦函数,的图象.3.正弦曲线、余弦曲线正弦函数的图象和余弦函数的图象分别叫做正弦函数和余弦曲线.它们是具有相同形状的“波浪起伏”的连续光滑曲线.例1-1:(1)作出函数的简图;(2)作出函数的简图.答案:(1)(2)例1-2:作出函数的简图.答案:知识点2:正弦函数、余弦函数的性质1.周期函数(1)定义:一般地,设函数的定义域为D,如果存在一个非零常数T,使得对每一个都有,且,那么函数就叫做周期函数.非零常数叫做这个函数的周期函数.(2)最小正周期:如果在周期函数的所有周期中存在一个最小的正数,那么这个最小正数就叫做的最小正数就叫做的最小正周期.2.正弦函数、余弦函数的性质正弦函数与余弦函数的图像与性质如下表:函数函数定义域RR值域[-1,1][-1,1]周期性最小正周期:最...