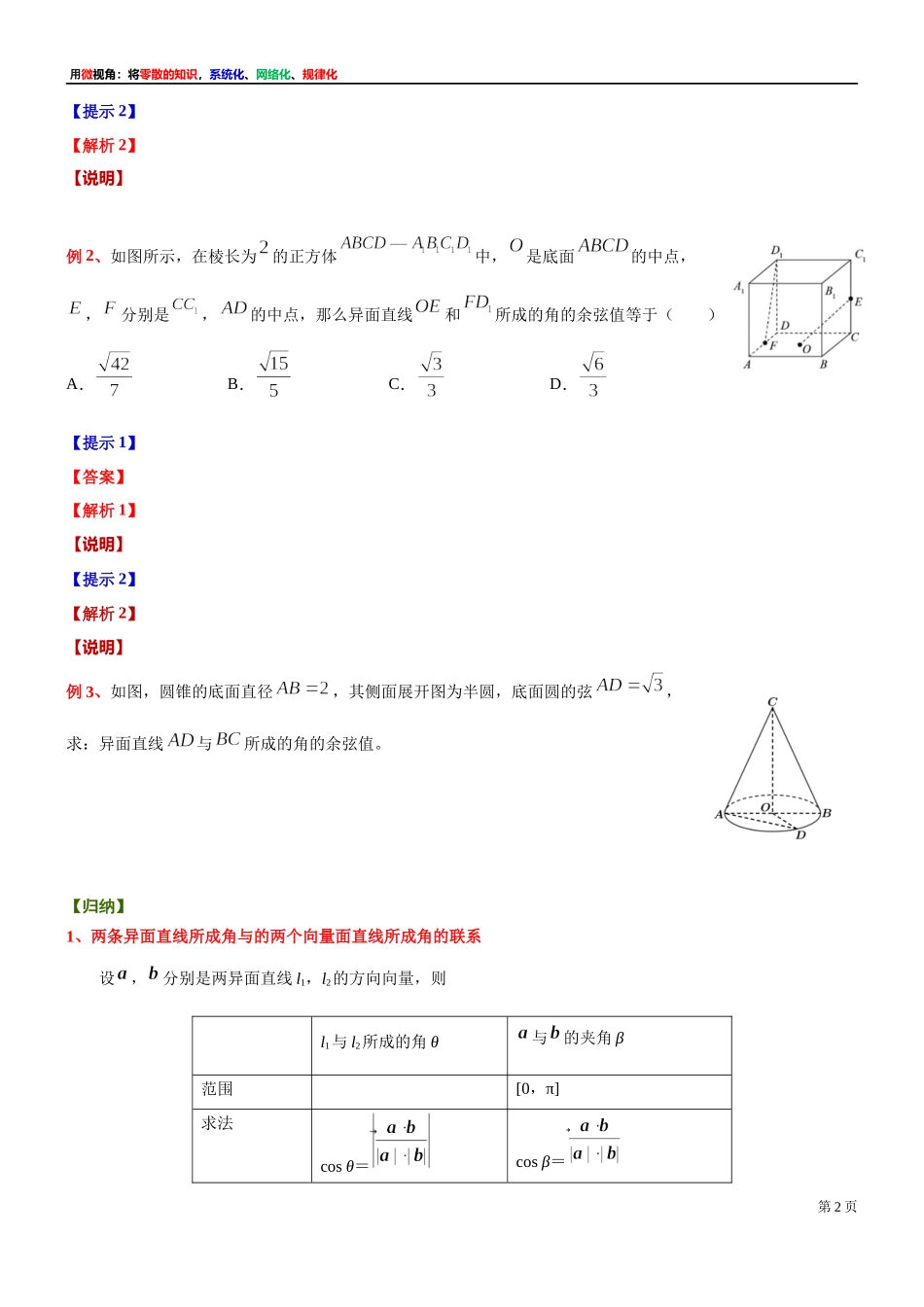
用微视角:将零散的知识,系统化、网络化、规律化【学生版】微专题:利用空间向量求异面直线所成的角1、两条异面直线所成的角①定义:设,是两条异面直线,过空间任一点作直线∥,∥,则与所夹的锐角或直角叫做与所成的角;②范围:两异面直线所成角θ的取值范围是;2、利用向量求异面直线所成的角(1)是几何法:作—证—算;(2)是向量法:把角的求解转化为向量运算,应注意体会两种方法的特点,“转化”是求异面直线所成角的关键,一般地,异面直线,的夹角β的余弦值为;3、用向量法求异面直线所成的角的步骤(1)建立空间直角坐标系(或确定不共面的三个非零向量为基向量);(2)求出两条直线的方向向量;(3)代入向量数量积公式求解;(4)归纳,回答(注意:异面直线所成的角与向量所成的角的差异);【注意】两条异面直线所成的角不一定是两直线的方向向量的夹角,即;【典例】例1、底面为正三角形的直棱柱中,,,,分别为,的中点,则异面直线与所成的角的余弦值为()A.B.C.D.【提示1】【答案】【解析1】第1页用微视角:将零散的知识,系统化、网络化、规律化【提示2】【解析2】【说明】例2、如图所示,在棱长为的正方体中,是底面的中点,,分别是,的中点,那么异面直线和所成的角的余弦值等于()A.B.C.D.【提示1】【答案】【解析1】【说明】【提示2】【解析2】【说明】例3、如图,圆锥的底面直径,其侧面展开图为半圆,底面圆的弦,求:异面直线与所成的角的余弦值。【归纳】1、两条异面直线所成角与的两个向量面直线所成角的联系设,分别是两异面直线l1,l2的方向向量,则l1与l2所成的角θ与的夹角β范围[0,π]求法cosθ=cosβ=第2页用微视角:将零散的知识,系统化、网络化、规律化1、向量法求两异面直线所成角的步骤(1)选好基底或建立空间直角坐标系;(2)求出两直线的方向向量,;(3)代入公式求解;【提醒】两异面直线所成角θ的范围是,两向量的夹角α的范围是[0,π],当两异面直线的方向向量的夹角为锐角或直角时,就是这两条异面直线所成的角;当两异面直线的方向向量的夹角为钝角时,其补角才是两异面直线所成的角;【即时练习】1、在长方体中,,,则异面直线与所成角的余弦值为()A.B.C.D.2、已知正方体中,,分别为,的中点,那么异面直线,所成角的余弦值为()A.B.C.D.3、如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=,BC=2,点D为BC的中点,则异面直线AD与A1C所成的角为4、如图,在三...