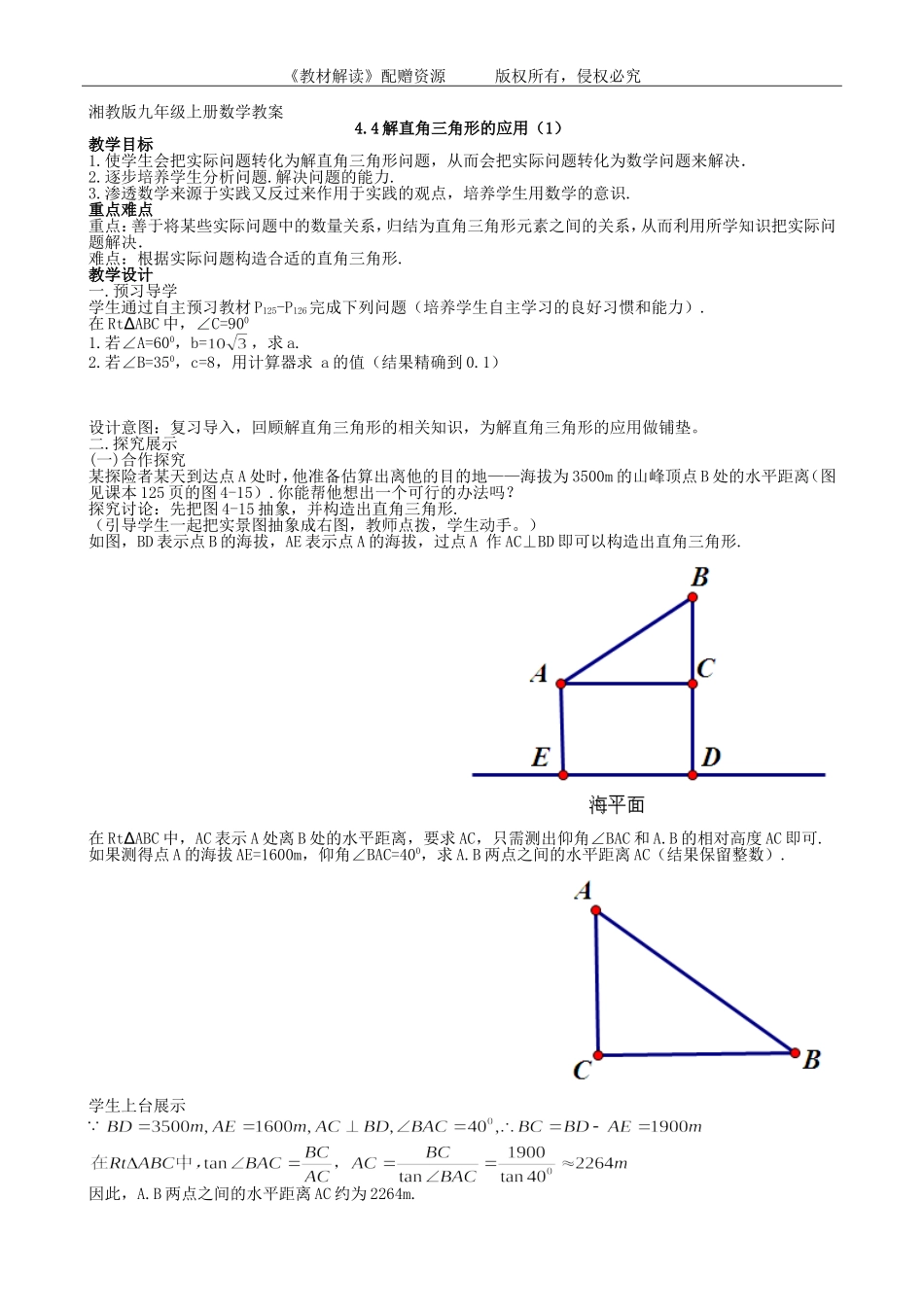
《教材解读》配赠资源版权所有,侵权必究湘教版九年级上册数学教案4.4解直角三角形的应用(1)教学目标1.使学生会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决.2.逐步培养学生分析问题.解决问题的能力.3.渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识.重点难点重点:善于将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.难点:根据实际问题构造合适的直角三角形.教学设计一.预习导学学生通过自主预习教材P125-P126完成下列问题(培养学生自主学习的良好习惯和能力).在RtABC∆中,∠C=9001.若∠A=600,b=,求a.2.若∠B=350,c=8,用计算器求a的值(结果精确到0.1)设计意图:复习导入,回顾解直角三角形的相关知识,为解直角三角形的应用做铺垫。二.探究展示(一)合作探究某探险者某天到达点A处时,他准备估算出离他的目的地——海拔为3500m的山峰顶点B处的水平距离(图见课本125页的图4-15).你能帮他想出一个可行的办法吗?探究讨论:先把图4-15抽象,并构造出直角三角形.(引导学生一起把实景图抽象成右图,教师点拨,学生动手。)如图,BD表示点B的海拔,AE表示点A的海拔,过点A作AC⊥BD即可以构造出直角三角形.在RtABC∆中,AC表示A处离B处的水平距离,要求AC,只需测出仰角∠BAC和A.B的相对高度AC即可.如果测得点A的海拔AE=1600m,仰角∠BAC=400,求A.B两点之间的水平距离AC(结果保留整数).学生上台展示因此,A.B两点之间的水平距离AC约为2264m.《教材解读》配赠资源版权所有,侵权必究(二)展示提升(首先组内讨论,然后分组上台讲解,其他学生补充、质疑,老师适时点拨、追问,引导学生总结解题方法).1.在离上海东方明珠塔底部1000m的A处,用仪器测得塔顶的仰角∠BAC为250,仪器距地面高AE为1.7m,求上海东方明珠塔的高度BD(结果精确到1m).设计意图:熟悉俯角、仰角的概念(都是视线与水平线的夹角),在解直角三角形题的基础上,稍加难度,学会用解直角三角形的相关知识,解决实际问题。2.某厂家新开发的一种电动车的大灯A射出的光线AB.AC与地面MN所成的夹角∠ABN、∠ACN分别为80和150,大灯A与地面的距离为1m,求该车大灯照亮地面的宽度BC(不考虑其他因素,结果精确到0.1m).设计意图:BC不是直角三角形的一边,所以不能直接求出。设计本题的目的在于让学生学会做辅助线构造直角三角形,并能通过解两个直角三角形来解决问题。通过质...